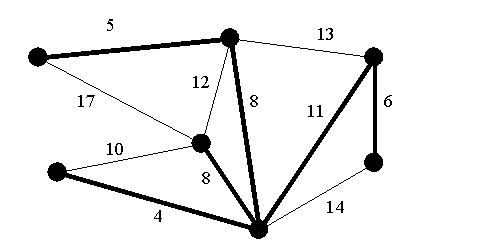
Remember the minimum spanning tree problem – you are given a graph G with weighted edges (real values on each edge) and the goal is to find a spanning tree T whose total weight is minimal. The minimum spanning tree is the least expensive way to connect up all the nodes. In the graph below, the minimum spanning tree is shown with heavy shaded edges.

Minimum spanning trees are useful for planning computer networks and for certain other kinds of resource and layout problems.
You have hopefully seen two deterministic algorithms for computing the minimum spanning tree: Prim’s and Kruskal’s algorithms. Both are greedy algorithms. They build the spanning tree by adding at each step the minimum weight edge that satisfies a certain property. Specifically:
Input: G = (V,E) which is a connected graph
Output: T, the minimum spanning tree
T ¬ empty graph
For i = 1 to |V| do
Let e be the minimum weight edge in G that touches T, and does not form a cycle with T.
T ¬ T + {e}
End
It is fairly easy to see how to implement this algorithm efficiently by maintaining a heap of the edges incident to T that haven’t been added yet, ordered by weight. If the graph has m edges and n vertices, the running time is O(m log n). The other deterministic algorithm is Kruskal’s:
Input: G = (V,E) which is a connected graph
Output: T, the minimum spanning tree
T ¬ empty graph
For i = 1 to |V| do
Let e be the minimum weight edge in G that does not form a cycle with T.
T ¬ T + {e}
End
The only difference between the two is that Kruskal doesn’t require the edge e to be connected to the evolving tree T. That means that T isn’t necessarily connected at intermediate steps in Kruskal’s algorithm. So strictly speaking the T in Kruskal’s algorithm is a forest and not a tree. Kruskal’s algorithm can also be implemented easily in O(m log n) time.
From looking at Prim and Kruskal, you can see that the general principle is similar. You pick the minimum weight edge that doesn’t create a cycle. The order that you pick these edges doesn’t matter much: whether they are minimum over all edges or just the edges incident to T.
e.g. suppose instead that for some forest T, you pick any vertex v not in T and add the minimum weight edge incident on v that doesn’t create a cycle. Then you are safe, because that edge must be in the minimum spanning tree.
The advantage of the last method is that you can do it in parallel. Suppose that T is empty for now. For every vertex v in the graph, find the minimum weight edge incident on v, and add it to T. All of these edges must be in the minimum spanning tree. You don’t need to check for cycles here because this scheme for choosing edges can’t possibly create a cycle. (Problem: prove that the set of minimum weight edges incident on all vertices cannot contain a cycle).
If T is not empty though, you do need to check for cycles, which complicates the algorithm and makes it harder to implement in parallel. Ideally, you would only deal with the empty T case. But there is a way to do that – by contracting the edges you have added. Contraction preserves the minimum spanning tree in a certain sense (you should be able to prove that yourself):
Let T be the minimum spanning tree of G, and let F be a subset of edges of T. Then if G’ is the graph that results by contracting the edges F, and T’ is the minimum spanning tree of G’, then T is the union of the edges in F and the edges in T’ (actually the "preimages" of the edges in T’ because their endpoints may have changed through contractions).
Contraction effectively makes the partial spanning forest T disappear, and so you can reapply the parallel edge selection once again. This technique is called Boruvka’s algorithm. It could be implemented like this:
Input: G = (V,E) which is a connected graph
Output: T, the minimum spanning tree
For each v in V do
Let e be the minimum weight edge that is incident on v
T ¬ T + {e}
G’ ¬ G with all edges in T contracted
T’ ¬ recursively compute the minimum spanning tree of G’
Return T + T’
First of all, notice that there are at least n/2 edges in T (or they could not touch all n vertices). So G’ has at least n/2 contracted edges, and therefore at most n/2 vertices. The recursion depth is therefore log2n. We claim that we can perform all the contractions at one level in O(m) time, where m is the number of edges in G. So overall, this algorithm has a running time of O(m log n) again.
But it would be nice if we could achieve O(m) running time (or O(n+m) to compute the minimum spanning forest for an unconnected graph). The weakness of Boruvka is that it reduces the number of vertices, but not necessarily the number of edges in each phase. You might remark that the number of edges is O(n2), and since n is decreasing, so is the upper bound on number of edges. That is true, but if m is "small" to begin with, e.g. O(n), then it takes O(log n) recursive steps before the upper bound caused by n will necessarily restrict the number of edges (the number of vertices has to decrease to about Ö n). Thus the running time really is O(m log n).
If we could somehow reduce the number of edges by some constant factor before the recursive call, then the problem sizes in the recursive call sequence would be a decreasing geometric series and the running time would be a constant times m. We will use probabilistic techniques to reduce the number of edges, and interleave those phases with Boruvka phases to reduce the number of vertices. First we need a notion of light and heavy edges.
Let F be any forest of edges in a graph G. For any two vertices u and v, let wF(u,v) denote the maximum weight of any edge along the unique path in F from u to v. If there is no path, wF(u,v) = ¥ . Note that the normal weight of the edge in G between u and v is w(u,v). Then
If w(u,v) > wF(u,v), we say the edge {u,v} is F-heavy.
If w(u,v) £ wF(u,v), then we say the edge {u,v} is F-light.
In particular, all the edges in F are F-light. Also, every edge in G is either F-heavy or F-light.
In order to reduce the number of edges in the graph, we will use the fact that a random subgraph of G has a "similar" minimum spanning tree. To be more precise, let G(p) be the subgraph of G obtained by adding each edge of G independently at random with probability p. we can say that
Lemma
Let F be the minimum spanning forest in the random graph G(p) obtained by keeping
edges of G with probability p. Then the expected number of F-light edges in G is at most
n/p.
Because we can delete all the F-heavy edges in G without changing the spanning tree of G, (even though F is the spanning forest for a subgraph of G) we can reduce the spanning tree calculation for G to a spanning tree calculation for a graph with a linear number of edges (n/p). That is the essence of the linear-time algorithm. Here it is:
Input: weight graph G with n vertices and m edges
Output: Minimum spanning forest F for G.
Analysis:
First notice that aside from recursive calls, this algorithm takes O(n+m) time, since
steps 1. and 2. take linear time in the number of edges in the graph. Step 4. isnt so
clear, but it also takes O(n+m) time because of the following theorem:
Theorem
Given a graph G and a forest T, all F-heavy edges in G can be identified in time
O(n+m)
Let T(n,m) be the running time of the algorithm in terms of the number of vertices n and number of edges m. Then the recursive call to compute the spanning forest G2 of takes T(n/8,m/2), while the recursive call on G3 takes T(n/8, n/4). Thus the recurrence for T(n,m) is
T(n,m) = T(n/8,m/2) + T(n/8, n/4) + O(n+m)
and you can solve this to obtain the overall running time T(n,m) = O(n+m).