CS174 Spring 99 Lecture 14 Summary

Data-Punctuated Token Trees (Berlekamp)

Fingerprints provide a fast and communication-efficient way to check whether two strings are identical or not. Rather than sending S and T over a network, you can send the fingerprint f(S) from one processor to the other, where it can be compared to f(T). But if two strings are slightly different (through editing or version changes) what do we do?

Data punctuated token trees provide a storage and communication-efficient way to compute and transmit the difference between two strings. The idea is to construct a tree with the characters of the string as leaves and such that each internal node holds the fingerprint of the subtree below it. Then comparing nodes gives a fast way to compare large substrings.

Fingerprint trees: First try

The most naïve way to build fingerprint trees is shown below. The characters of S are numbered in order S₁S₂…S_n.

Each non-leaf node contains the fingerprint of the substring below it. The tree is a complete binary tree (assuming n is a power of two). For the fingerprint functions discussed so far, it is easy to compute the value at a node from only the values of the two children. That is, if the fingerprint function is

Then we can combine fingerprints for the concatenation S+T of two k-byte strings S and T as

Then if we have fingerprint trees for identical strings S and T, all the internal nodes will have the same values. Now suppose we change one character S_j of S. The only changes occur in nodes that are ancestors of S_j.

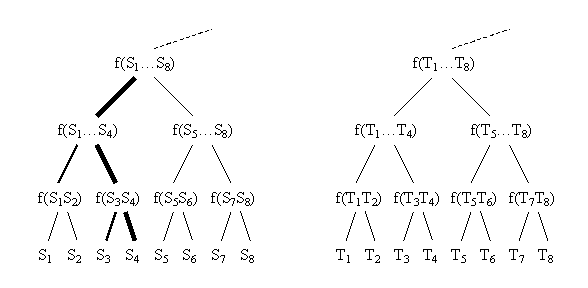
So to find the changed nodes, we start by comparing the roots of the two trees. Since they are different, we check all their children. In the example above S₄ has been changed and is now different from T₄. The left child of the top node in the tree above is different, so we check its children etc. We have shown two types of bold edges in the figure. The lighter bold edges indicate nodes that were checked. The heavy bold edges show nodes that were checked and found to be different. Eventually, we arrive at all the changed leaves. The time to find k changed nodes is O(k log n).

But there is a big problem with this scheme. If we add or delete a node S_j, all the nodes to the right of S_j and all their ancestors will need to be changed. That is, we will need to change W (n) nodes of the tree. The problem is that the alignment of nodes in this tree is derived strictly from the numbering of the characters in the sequence, and that can be changed by an insert or a delete.

The solution is to use a self-aligning fingerprint tree. We build a tree whose structure is determined by the data objects (characters) themselves. To do this, we need a binary-valued parity function on characters. The parity function doesn’t have to be the usual parity function (i.e. 1 for an odd, 0 for even), but any binary function that is 1 on about half the inputs and which has a "random" character. By this we mean that it is hard to predict the value of the parity function on any given input.

To be more precise, we will assume that B = {0,…,2^b-1} is the range of a b-bit character, and that

f_k: B^k ® B is a k-argument fingerprint function (which returns a character) and

P: B ® {0,1} is the parity function for characters.

Data-punctuated Trees

After we apply the parity function to the input characters, we get a stream of bits:

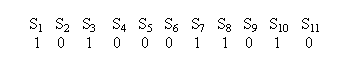
We use these bits to determine the alignment of the tree. First, we draw boundaries wherever there is a transition from a 1 to a 0. That is we draw vertical lines at those transitions

In between the vertical bars, the parity bits consists of a sequence of (at least one) 0’s and (at least one) 1’s. Each group becomes the set of children of a new node:

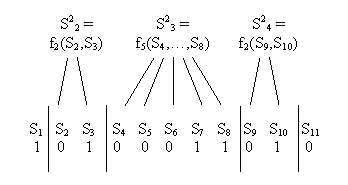
The new nodes themselves have character values, and are denoted as S²_k where 2 indicates that they are at the second level of the tree, and k is their left-right position at that level.

We then apply the parity function to the string S² = (S²₁,S²₂,…) producing a new binary sequence. We partition this sequence as above and compute the fingerprint of each group, producing the next level of the tree, S³ = (S³₁,S³₂,...). We continue moving up until there is a single node, at which point we have built a fingerprint tree. Each node contains the fingerprint of its children, but the number of children is variable. There must be at least two children (at least one 0 and one 1), but there is no upper limit.

In order to analyze these trees, we make a couple of assumptions:

1. The parity function is "pseudo-random" that is, it always produces the same output on a given input, but that output is irregular and hard to predict given the output. So the sequence of outputs on a sequence of distinct inputs looks like a random bit string.
2. The input data does not contain long substrings of duplicate characters. Because the parity function must produce the same output on the same input, a long string of identical input characters produces a long string of identical bits, which is clearly not random. We could guarantee that the input string satisfies this property by using run-length coding or some other compression scheme (we must be careful that the compression scheme preserves similarity, i.e. changing a few characters of the uncompressed string should change only a few characters of the compressed string).

Expected number of children

Because of the partitioning, the expected number of children is the expected number of bits between consecutive 1-to-0 transitions in a random binary string. Let this number be Z, we can express this number (carefully) as a sum of two geometric random variables X and Y. X equals the length of the sequence of contiguous zeros between the 1-to-0 transition and the 0-to-1 transition, and Y is the length of the sequence of contiguous ones between the 0-to-1 transition and the second 1-to-0 transition:

Note that for the usual definition of geometric r.v., X must start with the second zero (the first is zero by definition) which is a random choice, and it must finish with the first one. Similarly, Y starts with the second one (if there is one) and finishes with the next zero. But the result is the same as if we shifted X and Y one place to the left.

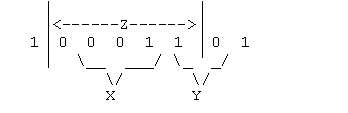
Since X is a geometric random variable with p = 0.5 its expected value E[X] = 1/p = 2. Similarly, E[Y] = 2. So the expected number of children is

The probability Pr[Z=k] = (k-1)2^-k, so it falls off sharply with increasing k. e.g. The probability that the number of children is 8 or greater is about 0.0625.

Since the degree is at least two (except for the first and last nodes at each level), the height of a fingerprint tree with N nodes is O(log N), and on average about log₄ N.

Edits to Data-Punctuated Trees

The important property of data-punctuated fingerprint trees is that local changes to the input string cause local changes to the tree. That is, a change, insert or delete to a leaf affects only the ancestor nodes (and a few nodes nearby). The number of changes is O(log N) where N is the length of the string. We give a simplified proof here:

Lemma

Let S^k_j-1,S^k_j,S^k_j+1 be a sequence of three consecutive nodes at level k. Then any change to these nodes (including removing any of them, or if all three are inserts) requires changes to at most three consecutive nodes at level k+1.

Proof

We note simply that there are at most 3 consecutive nodes at level k+1 whose values depend on S^k_j-1,S^k_j,S^k_j+1. Denote them S^k+1_i-1,S^k+1_i,S^k+1_i+1. Then S^k+1_i must be the parent of two or three nodes from S^k_j-1,S^k_j,S^k_j+1, while S^k+1_i-1 and S^k+1_i+1 must include neighboring nodes as well as (possibly) nodes from among S^k_j-1,S^k_j,S^k_j+1.

We cannot tighten this result. There are situations where changing the values of 3 nodes at level k does indeed change the values of 3 nodes at level k+1. For example, suppose we have the following setup before changes to the level k nodes (bit values are for the level k nodes):

And then when we make changes to the three level k nodes, the new picture is:

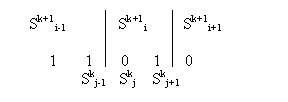
Both the 1-to-0 boundaries have moved, and that is why both S^k+1_i-1 and S^k+1_i+1 have changed. In other cases, we may end up with fewer than 3 nodes at level k+1. That is fine, the lemma states that at most 3 nodes at level k+1 can change.

When we insert or delete or change a leaf node (i.e. we modify the original string), then this is a special case of changing 3 consecutive nodes at level 1 of the tree. In fact a single change can only cause two changed nodes at the next level, but there may be three at the level above. Thus the total number of changed nodes is at most 3 times the height of the tree, which is O(log N). In fact, 3 changed nodes at each level is quite pessimistic. More typically, changing one or two nodes at level k will lead to only one or two changed nodes at the next level, so the expected number of changed nodes per level in somewhere in between one and two.

In operation, data-punctuated trees work like the fingerprint trees discussed earlier. We transmit first the root, then if it differs, we transmit its children, and then the children of child nodes that differ etc. Thus, if there are k changes between documents, we need to transmit O(k log N) nodes, and fewer if the changes are localized in the documents.