Optimal Solutions for Sparse Principal Component Analysis
Download: .pdf
Authors: A. d'Aspremont, F. Bach, L. El Ghaoui.
Status: Journal of Machine Learning Research, 9(Jul):1269–1294, 2008.
Abstract: Given a sample covariance matrix, we examine the problem of maximizing the variance explained by a linear combination of the input variables while constraining the number of nonzero coefficients in this combination. This is known as sparse principal component analysis and has a wide array of applications in machine learning and engineering. We formulate a new semidefinite relaxation to this problem and derive a greedy algorithm that computes a full set of good solutions for all target numbers of non zero coefficients, with total complexity
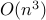 , where
, where 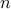 is the number of variables. We then use the same relaxation to derive sufficient conditions for global optimality of a solution, which can be tested in
is the number of variables. We then use the same relaxation to derive sufficient conditions for global optimality of a solution, which can be tested in 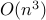 per pattern. We discuss applications in subset selection and sparse recovery and show on artificial examples and biological data that our algorithm does provide globally optimal solutions in many cases.
per pattern. We discuss applications in subset selection and sparse recovery and show on artificial examples and biological data that our algorithm does provide globally optimal solutions in many cases.
Related entries:
A. d'Aspremont, F. Bach, L. El Ghaoui. Optimal Solutions for Sparse Principal Component Analysis, preprint on arXiv.
L. El Ghaoui. On the Quality of a Semidefinite Programming Bound for Sparse Principal Component Analysis.
A. d'Aspremont, F. Bach, L. El Ghaoui. Full regularization path for sparse principal component analysis, Proc. ICML, 2007.
Code: PathSPCA.
Bibtex reference:
@article{ABE:08a,
Author = {A. d'Aspremont, F. Bach and L. {El Ghaoui}},
Journal = {Journal of Machine Learning Research},
Month = {July},
Pages = {1269--1294},
Title = {Optimal Solutions for Sparse Principal Component Analysis},
Volume = {9},
Year = {2008}}