The IEEE floating point standards prescribe precisely how floating point numbers should be represented, and the results of all operations on floating point numbers. There are two standards: IEEE 754 is for binary arithmetic, and IEEE 854 covers decimal arithmetic as well. We will only discuss IEEE 754, which has been adopted almost universally by computer manufacturers. Indeed, except for older, obsolete architectures (such as IBM 370 and VAX), and the Cray XMP, YMP, 2, C90 and first generation T90, all other machines, including PCs, workstations, and parallel machines built from the same microprocessors, use IEEE arithmetic. The next Cray T90 is supposed to implement IEEE arithmetic.
So the good news is that essentially all new computers will be using the same floating point arithmetic in the near future, and almost all do now, with the important exception of Cray. This simplifies code development, especially portable code development, as well as some important rounding error analyses, as we will illustrate below.
Unfortunately, not all manufacturers implement every detail of IEEE arithmetic the same way. Everyone does indeed represent numbers with the same bit patterns, and rounds results correctly (or tries to!). But exceptional conditions (like 1/0, sqrt(-1) etc.), whose semantics are also specified in detail by the IEEE standard, are not always handled the same way. It turns out that many manufacturers believe (sometimes rightly and sometimes wrongly) that conforming to every detail of IEEE arithmetic would make their machines either a bit slower or a bit more expensive, enough so make them less attractive in the marketplace. In particular, machines are often sold on the basis of how fast they execute certain standard benchmarks, like the Linpack Benchmark, which do not generate exceptions, so exception handling often gets short shrift. We will discuss the impact of this on code development.
Floating point formats
Name of format Bytes to Number of bits Macheps Number of Approx range
store in significand exponent bits
-------------- -------- -------------- ------- ------------- ------------
Single 4 24 2^(-24) ~ 1e-7 8 10^(+-38)
Double 8 53 2^(-53) ~ 1e-16 11 >=10^(+-308)
Double extended >=10 >=64 <=2^(-64) ~ 1e-19 >=15 >=10^(+-4932)
Quadruple 16 113 2^(-113)~ 1e-34 15 10^(+-4932)
Macheps is short for "machine epsilon", and is used below for roundoff error analysis.
The distance between 1 and the next larger floating point number is 2*macheps.
When the exponent has neither its largest possible value (a string of all ones) nor its smallest possible value (a string of all zeros), then the significand is necessarily normalized, and lies in [1,2).
When the exponent has its largest possible value (all ones), the floating point number is either +infinity, -infinity, or NAN (not-a-number); we discuss these further below under exceptions. The largest finite floating point number is called the overflow threshold.
When the exponent has its smallest possible value (all zeros), the significand may have leading zeros, and is called either subnormal or denormal (unless it is exactly zero). The subnormal floating point numbers represent very tiny numbers between the smallest nonzero normalized floating point number (the underflow threshold) and zero. An operation that underflows yields a subnormal number or possibly zero; this is called gradual underflow. The alternative, simply returning a zero, is called flush to zero. When the significand is zero, the floating point number is +-0.
The basic operations specified by IEEE arithmetic are first and foremost addition, subtraction, multiplication and division. Square roots and remainders are also included. The default rounding for these operations is "to nearest even". This means that the floating point result fl(a op b) of the exact operation (a op b) is the nearest floating point number to (a op b), breaking ties by rounding to the floating point number whose bottom bit is zero (the "even" one). It is also possible to round up, round down, or truncate (round towards zero). Rounding up and down are useful for interval arithmetic, which can provide guaranteed error bounds; unfortunately most languages and/or compilers provide no access to the status flag which can select the rounding direction.
Other operations include binary-decimal conversion, floating point-integer conversions, and conversions among floating point formats, and comparisons.
(*) fl(a op b) = (1+ eps)*(a op b) provided fl(a op b) neither overflows nor underflowswhere
(a op b) is the exact result of the operation, where op is one of +, -, * and /
fl(a op b) is the floating point result
| eps | <= macheps
To incorporate underflow, we may write
fl(a op b) = (1+ eps)*(a op b) + eta provided fl(a op b) does not overflowwhere
| eta | <= macheps * underflow_threshold
On machines which do not implement gradual underflow (including some IEEE machines which
have an option to perform flush-to-zero arithmetic instead), the corresponding error
formula is
| eta | <= underflow_threshold
i.e. the error is 1/macheps times larger.
(**) fl(a +- b) = ( (1+eps1)*a ) +- ( (1+eps2)*b ) provided fl(a +- b ) neither overflows
nor underflows
In particular, this means that if a and b are nearly equal, so a-b is much smaller than
either a or b (this is called extreme cancellation),
then the relative error may be quite large. For example when subtracting
1-x, where x is the next smaller floating point number than 1, the answer is twice too
large on a Cray C90, and 0 when it should be nonzero on a Cray 2.
This happens because when y's significand is shifted right to line its binary point up with 1's binary point, prior to actually subtracting the significands, any bits shifted past the least significant bit of 1 are simply thrown away (differently on a C90 and Cray 2), rather than participating in the subtraction. On IEEE machines, there is a so-called guard digit (actually 3 of them) to store any bits shifted this way, so they can participate in the subtraction.
This source of error has little effect on most problems in numerical linear algebra, but there are some important exceptions, as illustrated below.
error = alg(x) - f(x)
Rather than trying to compute the error directly, we proceed as follows.
We first try to show that alg(x) is numerically stable, that is alg(x) is nearly the exact result f(x+e) of a slightly perturbed problem x+e:
alg(x) ~ f(x+e) where e is small
Second, assuming f(x) is a smooth function at x, we approximate f(x) by a first-order Taylor expansion near x:
f(x+e) ~ f(x) + e*f'(x)
Combining the last two expressions yields
error = alg(x) - f(x)
~ f(x+e) - f(x)
~ f(x) + e*f'(x) - f(x)
= e*f'(x)
Thus, we have expressed the error as a product of a small quantity e and the derivative
f'(x). e is usually called the backward error of the algorithm. f'(x), which
depends only on f and not on the algorithm, is called the condition number.
In other words, the error is approximately the product of the backward error and
the condition number. This approach is ubiquitous in numerical linear algebra,
where x and f(x) are usually vectors and/or matrices, and we use norms to bound the
error:
|| error || <~ || e || * || f'(x) ||
(The norm of a vector ||v|| or matrix ||M|| might simply be the root-sum-of-squares
of its entries, for example.)
Computing || f'(x) || exactly is often as expensive as solving the original problem.
Therefore we often settle for an approximation; this is called
condition estimation.
Roundoff error analysis is needed to show that e is small. We illustrate with a few examples.

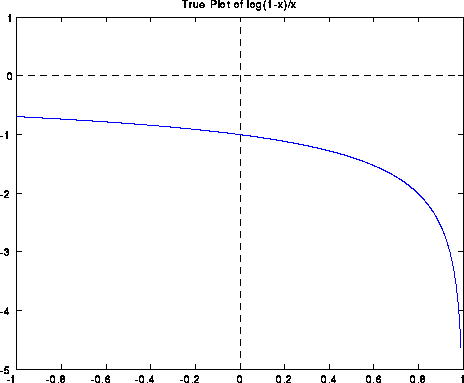
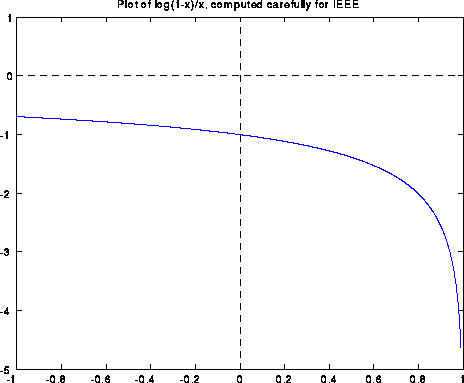
If we evaluate log(1-x)/x in IEEE floating point arithmetic using this formula (except for the special case f(0)=-1), the computed graph is shown below. Note that the answer is quite wrong near x=0, with a spike going from -2 to 0:

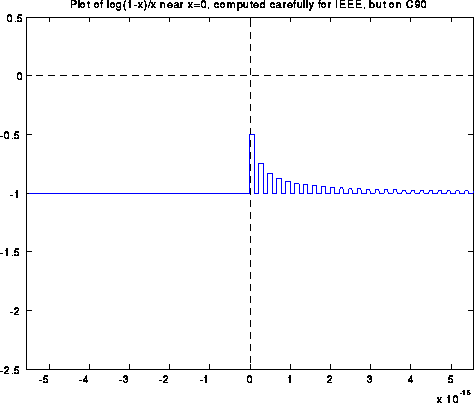
Blowing up the graph near x=0 shows a sort of periodic behavior:
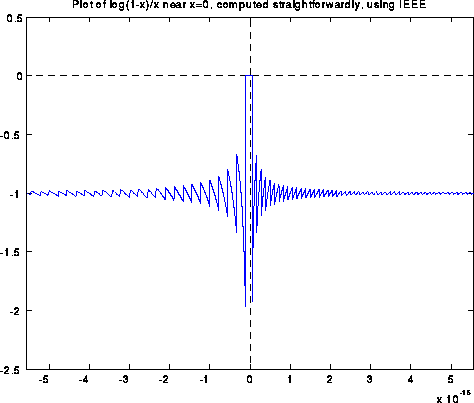
Blowing the graph up even more yields the following picture. To hint at what is going on, we have made green tic marks at all x values such that 1-x is an exact floating point number. The red tic marks are exactly half way in between the green tic marks, and are the thresholds where fl(1-x) suddenly changes from one floating point value to the next.

When x is tiny, log(1-x) is very close to -x. Said another way, when y is very close to 1, log(y) is very close to y-1. The next graph shows ((1-x)-1)/x, as computed in floating point. In exact arithmetic, this expression simplies to -1. But in floating point, it yields exactly the same picture as before:
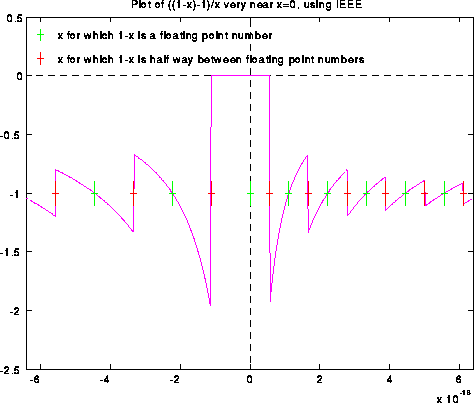
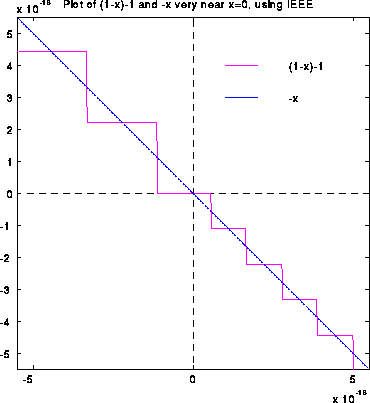
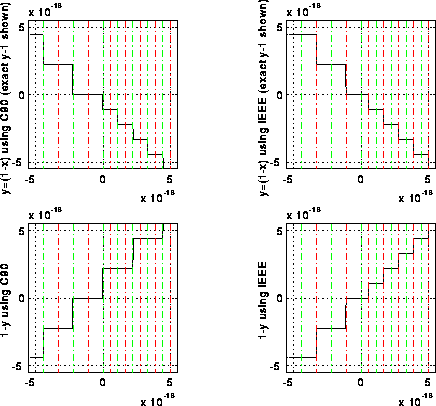
The next graph shows both (1-x)-1 and -x (both computed in floating point) on the same graph. Their quotient is what was shown in the last graph. It is easy to see why the quotient is far from -1: When x is tiny, fl(1-x) can only take on a few discrete values near 1, so fl(fl(1-x)-1) can in turn only take on a few discrete values, whereas x more nearly takes on a continuum of values.
Here is a different algorithm for f(x) which computes it quite precisely in IEEE arithmetic:
y=1-x
if y == 1,
f = -1
else
f = log(y)/(1-y)
endif
In real arithmetic, the algorithm is clearly equivalent to f = log(1-x)/x (except at x=0, where
it has the right limiting value). The graph of this function is shown below; it has no
difficulty near x=0.
This algorithm is backward stable, because it nearly computes log(1-(x+e))/(x+e), where e is small (on the order of of macheps); this makes the very reasonable assumption that the logarithm function is implemented accurately (this is not difficult). We invite the reader to supply a proof. (Hint: when x is small, there is no roundoff error committed when computing fl(1-y).)
Unfortunately, this improved algorithm is not backward stable on the Cray C90, as illustrated in the graph below, which only shows the graph for x near 0:
The subsequent plot is a bigger blowup near x=0, with floating point numbers of the form 1-x marked as before.

The following plots show intermediate results in the computation, both on an IEEE machine and on the Cray, for contrast. The final result on an IEEE machine is the quotient of the two values plotted in the two rightmost graphs; their quotient is clearly -1. The final result on a C90 is the quotient of the two values plotted in the two leftmost graphs; their quotient is clearly not -1 for x>0.
The problem lies in the fact that fl(1-y) is off by a factor of up to 2 when y is near 1 on a C90, whereas fl(1-y) is exact in IEEE arithmetic. The cure on a C90 is to replace
y = 1-x
by
y = .5 + (.5 - x)
and
f = log(y)/(1-y)
by
f = log(y)/(.5+(.5-y))
The reader is invited to prove why this works, and to rejoice that the imminent universality of IEEE arithmetic will make such tricks unnecessary.
x = ( D - lambda*I )^(-1) * z
Unfortunately, this formula is quite inaccurate when there are other eigenvalues
very close to lambda. In particular, eigenvectors of different, but nearby, eigenvalues are
not guaranteed to be orthogonal, which is essential for stability.
This difficulty was attacked by Sorensen, Tang, Kahan and others, and proposed solutions were
based on using double the input precision for certain critical parts of the calculation.
When the input precision is already double, this would require quadruple, which is not
widely available; this was the major stumbling block to widespread adoption of this algorithm
for many years.
Finally, in 1992 Eisenstat and Gu nearly completely overcame this problem by using a different, stable formula, now incorporated in LAPACK routine sstedc (and slaed3, which sstedc calls). We refer the reader to the paper by Gu and Eisenstat cited below for details. Here we will just examine the kernel of their formula
(*) x(i) = prod_{j=1 to n except i} q(i,j) / ( lambda(i) - lambda(j) )
where q(i,j) is some other (accurately) computed quantity. Stability depends on this
formula being evaluated accurately.
With IEEE arithmetic we may apply error analysis formula (*) above. Assuming for simplicity that q(i,j) is exact, we see that the computed x(i) differs from the true x(i) by a factor f, where f is the product of 2n-1 different terms of the form 1+eps, |eps| <= macheps. Thus x(i) is computed to high relative accuracy as desired.
With Cray arithmetic, on the other hand, if some difference lambda(i) - lambda(j) undergoes extreme cancellation, it may not be computed accurately. If q(i,j) is also small, the factor q(i,j) / ( lambda(i) - lambda(j) ) may be O(1) and completely wrong, so that x(i) is completely wrong. This can indeed occur, and this temporarily prevented us from incorporating divide-and-conquer into LAPACK, until we figured out what to do.
The fix for this problem was proposed by W. Kahan, who pointed out that if no lambda(i) has a nonzero least significant bit, then when extreme cancellation occurs no information is lost by shifting. Thus, simply setting the bottommost bit of each lambda(i) to zero, a tiny error, would fix the problem. Doing this in a portable way, that would run whether compiled on a Cray, PC or any other machine, required the following trick: It turns out that computing
lambda = ( lambda + lambda ) - lambda
has no effect on lambda on any binary machine which rounds in any reasonable way (barring
overflow). But on a Cray, it makes the bottom bit of lambda zero; the reader is invited
to show why.
This still does not explain the ultimate appearance of the LAPACK code. It turns out that many aggressive optimizing compilers will examine the expression above, and simply throw it away, because in exact arithmetic, it obviously would have no effect. To try to prevent this, (lambda+lambda) is actually computed by a function call, where the function is compiled at a lower level of optimization. This is still no guarantee, but we hope that by the time compilers become aggressive enough for this to be a problem, non-IEEE arithmetics will have disappeared.
As a historical note, for a while we considered implementing this algorithm in doubled precision which represents double precision quantities as a pair (upper,lower) of single precision quantities, and manipulates these pairs. The attraction is that if the input precision is already double, this simulates quadruple, letting us use the same algorithm in all precisions. Algorithms for this simulation are well known, but require a guard digit during addition and subtraction to be reasonably efficient. So the Cray's lack of a guard digit made this approach unattractive too.
z = arccos( x/sqrt(x^2+y^2) )
An enigmatic run-time error was generated, which he (and several company engineers)
finally tracked down to the fact that the computed value of x/sqrt(x^2+y^2) exceeded 1,
to which arccos() subsequently objected. This occurred on the Cray because of
sloppy rounding in the multiplication, division, and square root functions. Barring
over/underflow, it can not occur using IEEE arithmetic. The user is invited to find a proof.
A main contribution of IEEE arithmetic was to standardize on how exceptions are handled. There are five kinds of exceptions, as listed in the table below. The default response for all 5 types is to set a sticky status flag, and continue computing the the default result listed below. The status flag can be read by the user, and remains set until reset by the user (hence "sticky").
Exception Name Cause Default Result
-------------- ----- --------------
Overflow Result too large to represent Return +-Infinity
as a normalized number
Underflow Result too small to represent Return subnormal
as a nonzero normalized number number or 0
Divide-by-zero Computing x/0, where x is Return +-infinity
finite and nonzero
Invalid infinity-infinity, 0*infinity, NAN
infinity/infinity, 0/0, sqrt(-1),
x rem 0, infinity rem y,
comparison with NAN,
impossible binary-decimal conversion
Inexact A rounding error occurred rounded result
Alternatively, the IEEE standard recommends, but does not mandate, an alternative
response to an exception, namely trapping. This means interrupting execution
and jumping to another piece of code, possibly written by the user. In other words,
it does not merely mean jumping to the operating system, printing an error message,
and stopping, although this is indeed what most systems do. In principle, one could
branch to an entirely different algorithm to solve the problem, and continue
computing. The default response and sticky flags also provide this capability, but
the user must check for exceptions and branch explicitly.
This is the area where the most liberties are taken with implementations of IEEE arithmetic, since a complete implementation of all IEEE recommendations could impact programming languages, compilers, and operating systems. Also, interrupting precisely when an operation occurs is very difficult, when many operations are in partial state of execution in a pipelined execution unit; one either needs to have a complex enough system to back out of all the partially executed operations, or abandon many effective forms of pipelining.
We illustrate this paradigm with two examples below. It is effective on many machines, except that on machines which implement arithmetic with infinities and NANs very slowly, the worst case running time (as opposed to the average), could be quite slow. See the paper by Demmel and Li in the references for details.
|| computed x - true x ||
------------------------- <= ||A|| * ||inv(A)|| * macheps
|| computed x ||
The problem is to estimate || inv(A) || without computing inv(A) explicitly,
which would usually be more expensive than solving Ax=b in the first place.
LAPACK and other packages use an optimization approach which attempt to find
a unit vector z, such that || inv(A)*z || is as large as possible; this typically
requires a handful of solutions of linear systems of the form A*y=z, for carefully
chosen z vectors. If we have already done Gaussian elimination and factored
the matrix A into the product A=L*U of triangular matrices, the extra work involved in
condition estimation is usually negligible.
This is implemented in LAPACK routine
sgecon.f.
Thus, the inner loop of the algorithm requires the solution of triangular linear systems (with matrices L and U), where we expect the solution to be large. This is where exceptions come in. When A is nearly singular, so the computed solution is quite large, overflows are most likely. But if A is nearly singular, this is precisely when the user is most likely to want to do condition estimation. Therefore, we cannot simply call the existing, manufacturer-supplied, highly-optimized triangular system solver in the BLAS, because it may overflow. Therefore, in LAPACK we call our own complicated, slow and reliable alternative slatrs.f, which is careful to scale inside the inner loop to avoid possible exceptions.
Applying our three-point paradigm to this situation yields the algorithm
The result is an algorithm which is 1.5 to 5 times faster than the old one on a Sun 4/260, 1.6 to 9.3 times faster on a DEC Alpha, and 2.55 to 4.21 times faster on a Cray C90. A Cray C90 does not have IEEE exception handling, but these speedups were obtained in the most common case where no exceptions occurred. Thus, for the Cray, it measures the speed penalty paid on Cray by not having exception handling.
[ a(1) b(1) ]
[ b(1) a(2) b(2) ]
T = [ ... ... ... ]
[ b(n-1) a(n-1) b(n) ]
[ b(n) a(n) ]
and s is a shift, then barring exceptions the following simple algorithm counts the
number of eigenvalues of T less than s:
count = 0
b(0) = 0
d = 1
for i = 1 to n
d = a(i) - s - b(i-1)^2/d
if (d<0) count = count + 1
end for
To make this code robust, we must take into account exceptions in the inner loop.
For example, if s were an eigenvalue of the leading k-by-k submatrix of T, then
(in exact arithmetic) the k-th value of d would be exactly zero.
Assuming we prescale T so its largest entry is neither too large nor too small
(making ||T|| equal to the fourth root of the overflow threshold is a good value),
then the following code is robust across all machines, and is currently in LAPACK
routine slaebz.f (called by
sstebz):
count = 0
b(0) = 0
d = 1
pivmin = sqrt(underflow_threshold)
for i = 1 to n
d = a(i) - s - b(i-1)^2/d
if (abs(d) < pivmin) d = -pivmin ... guarantees division by |d| not too small
if (d < 0) count = count + 1
end for
However, this runs about 14% to 47% slower than the simpler algorithm above. With IEEE
arithmetic, it turns out that the first algorithm is perfectly correct even when d becomes
zero. The result is that the next d will be +-infinity, and on the subsequent iteration
-b(i-1)^2/d will be zero again. One can show that this yields accurate and reliable
results; see the reference below.