
The spirit of this lecture is to find the fastest possible parallel algorithm for a variety of problems, not concerning ourselves with how many processors are needed, or whether our algorithms are numerically stable. As a result, some of our algorithms will be impractical, and mostly of academic interest (and we are academics!). Others are of great practical interest, and in fact are used in every existing microprocessor hardware design.
All logarithms are to the base 2.

y0 = x0
y1 = x0 + x1
y2 = x0 + x1 + x2
...
yp-1 = x0 + x1 + x2 + ... + xp-1
In what follows, the + operator could be replaced by any other associative
operator (product, max, min, matrix multiplication, ...) but for simplicity
we discuss addition. We show how to compute y0 through yp-1 in 2*log_2 p -1
steps using a tree.
There are two ways to see the pattern. Perhaps the simplest is the following, where we use the abbreviation i:j, where i <= j, to mean the sum ai+...+aj. The final values at each node are indicated in blue.
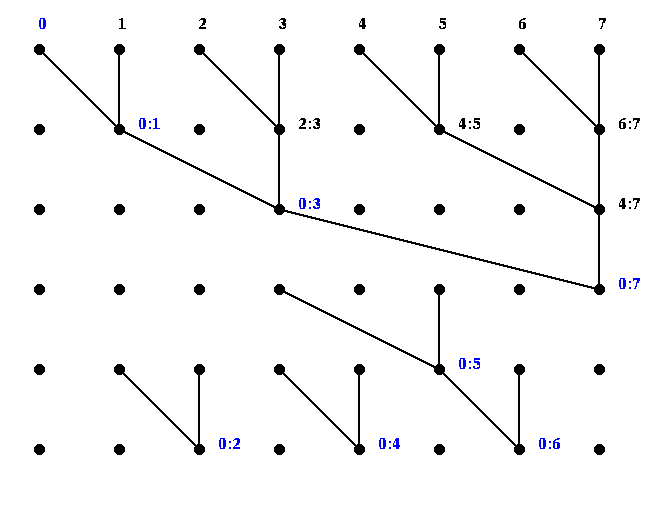
This is actually mapped onto a tree as follows. There is an "up-the-tree" phase, and a "down-the-tree" phase. On the way up, each internal tree node runs the following algorithm.
On the way down, this is the algorithm: On the way up, one can show by induction on the tree that M contains the sum of the leaves of the left subtree at each node. On the way down, one can show by induction that the value T obtained from the parent is the sum of all the leaf nodes to the left of the subtree rooted at the parent. Finally, the value at each leaf is added to the value received from the parent to get the final value. Here is an example.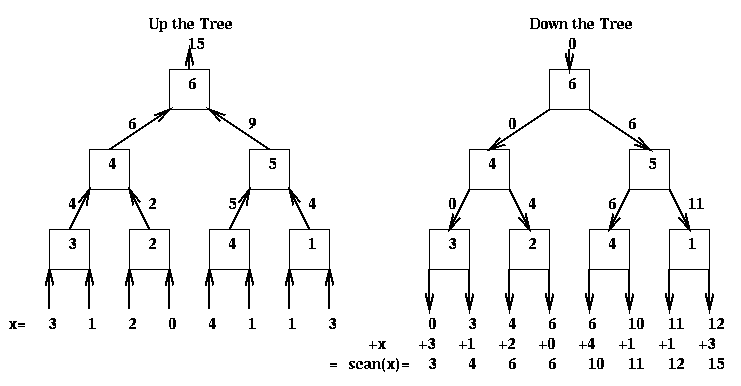
for all (1 <= i,j,k <= n ) C(i,j,k) = A(i,k)*B(k,j)
for all (1 <= i,j <= n) C(i,j) = sum_{k=1}^n C(i,j,k)
The first step can be done in 1 time step with n^3 processors, and the
second in log n times steps with (n^3)/2 processors.
Lemma 1.
inv ( [ A 0 ] ) = [ inv(A) 0 ]
( [ C B ] ) [ -inv(B)*C*inv(A) inv(B) ]
This leads immediately to the following simple divide-and-conquer algorithm,
where for simplicity we assume the dimension n of T is a power of 2:
function TriInv(T)
if T is 1-by-1 then
return 1/T
else
let [ A 0 ] = T
[ C B ]
in parallel do { invA = TriInv(A); invB = TriInv(B) }
newC = -invB*C*invA
return [ invA 0 ]
[ newC invB ]
endif
We compute the running time as follows. Let n=2^m denote the dimension of T,
and let TriTime(n) be the running time. Then
TriTime(n) = TriTime(n/2) ... time for two parallel calls for TriInv()
+ O(log n) ... time for two matrix multiplies
Change variables from n to m = log n, to get
TriTime(m) = TriTime(m-1) + O(m)
= O(m^2) = O( log^2 n )
as desired.
Lemma 2. The Cayley-Hamilton Theorem. Let p(x) = determinant(x*I - A) be the characteristic polynomial of A, whose roots are, by definition, the eigenvalues lambda(1), ... , lambda(n) of A. Write p(x) = x^n + c(1)*x^(n-1) + ... + c(n). Then
p(A) = A^n + c(1)*A^(n-1) + ... + c(n)*I = 0
and c(n) = +-determinant(A).
The proof may be found in any linear algebra textbook.
If A is nonsingular, so c(n) != 0, the Cayley-Hamilton theorem lets us express inv(A) as a polynomial in A, simply by multiplying the equation p(A)=0 by inv(A) and solving for inv(A):
inv(A)*p(A) = A^(n-1) + c(1)*A^(n-2) + ... + c(n-1)*I + c(n)*inv(A) = 0
or
inv(A) = (A^(n-1) + c(1)*A^(n-2) + ... + c(n-1)*I)/(-c(n))
If we could somehow compute the coefficients c(i), then we could use
this formula to evaluate inv(A). Then next Lemma gives a way to do this.
Lemma 3. Newton's Identities. Let p(x) = x^n + c(1) * x^(n-1) + ... + c(n) be a monic polynomial with degree n, with roots lambda(1), lambda(2), ..., lambda(n). Let s(k) = sum_{i=1}^n lambda(i)^k, the sum of the k-th powers of the roots. Then the c(i)'s and s(i)'s satisfy the following n-by-n lower triangular system of linear equations:
[ 1 ] [ c(1) ] [ -s(1) ]
[ s(1) 2 ] [ c(2) ] [ -s(2) ]
[ s(2) s(1) 3 ] * [ . ] = [ . ]
[ s(3) s(2) s(1) 4 ] [ . ] [ . ]
[ . . . . . ] [ . ] [ . ]
[ s(n-1) . . . s(1) n ] [ c(n) ] [ -s(n) ]
The diagonal of the triangular matrix consists of consecutive integers,
and the i-th subdiagonal is equal to s(i). Thus, given the s(k),
we can solve this triangular system to get the polynomial coefficients.
Proof. We sketch the proof. Details may be found in "Parallel and Distributed Computation" by Bertsekas and Tsitsiklis, Prentice-Hall, 1989. We expand the derivative p'(x) in powers of x in two different ways, and equate coefficients of like powers of x in each expansion. The first expansion is simply
p'(x) = n*x^(n-1) + c(1)*(n-1)*x^(n-2) + ... + c(n-1)The second expansion begins with p(x) = prod_{i=1}^n (x-lambda(i)) to get
p'(x) = sum_{i=1}^n [ p(x) / (x-lambda(i)) ]
For large enough x, we may expand
1 / (x - lambda(i)) = (1/x) * ( 1 / ( 1 - (lambda(i)/x) ) )
= (1/x) * sum_{k=0}^{infinity} (lambda(i)/x)^k
Inserting this in the last expansion for p'(x), and reversing the order of
summation, yields
p'(x) = (p(x) / x) * sum_{i=1}^n sum_{k=0}^{infinity} (lambda(i)/x)^k
= (p(x) / x) * sum_{k=0}^{infinity} sum_{i=1}^n (lambda(i)/x)^k
= (p(x) / x) * sum_{k=0}^{infinity} s(k)/x^k
where s(0)=1. Now substitute p(x) = x^n + ... + c(n), and multiply out to get
the second expansion.
This completes the proof.
To be able to use Lemma 3 to get the coefficients of the characteristic polynomial, we need to compute the s(k), the sums of powers of eigenvalues. The next two lemmas show how to do this.
Lemma 4. The trace of the matrix A is defined as tr(A) = sum_{i=1}^n A(i,i), the sum of the diagonal entries. Then tr(A) = sum_{i=1}^n lambda(i), the sum of the eigenvalues.
Proof. We sketch the proof. As above, we may write the characteristic polynomial p(x) in two ways:
p(x) = x^n + c(1)*x^(n-1) + ... + c(n) = prod_{i=1}^n (x - lambda(i))
By examining the expansion of determinant(x*I-A), it is easy to see
that the coefficient of x^(n-1), c(1) = -tr(A).
By examining prod_{i=1}^n (x - lambda(i)), it is easy to see that the
coefficient of x^(n-1) may also be written -sum_{i=1}^n lambda(i).
This completes the proof.
Lemma 4. If the eigenvalues of A are lambda(1), ... , lambda(n), then the eigenvalues of A^k are lambda(1)^k , ... , lambda(n)^k.
Proof. If A*x = lambda*x, then A^2*x = A*lambda*x = lambda^2*x, and similarly A^k*x = lambda^k*x. This completes the proof.
Thus, s(k) = sum_{i=1}^n lambda(i)^k is simply the trace of A^k. Now we have all the ingredients we need for our algorithm.
Csanky's Algorithm for matrix inversion
1) Compute the powers A^2, A^3, ... , A^(n-1) using parallel prefix.
2) Compute the traces s(k) = tr(A^k)
3) Solve the Newton Identities for the c(i).
4) Evaluate inv(A) using the formula from the Cayley-Hamilton Theorem.
Here is the complexity analysis. In step 1, parallel prefix requires log n parallel steps to compute all the powers A^k. Each parallel step requires n-by-n matrix multiplication, which costs O(log n), for a total time of O(log^2 n). Step 2 takes log n steps to compute n sums. Step 3 takes O(log^2 n) steps using our divide-and-conquer algorithm for triangular matrix inversion. Finally, step 4 takes log(n) steps to evaluate the formula for inv(A).
This algorithm is numerically quite unstable. In a numerical experiment, we used this algorithm to invert 3*I_n, where I_n is the n-by-n identity matrix. We used double precision, i.e. about 16 decimal digits of accuracy. For n>50, no correct digits were obtained. The source of the instability is the sizes of the terms c(i)*A^(n-i-1) which must be summed to get inv(A). These are enormous, both because A^(n-i-1) and because c(i) is enormous. These terms are added and we expect the sum to be (1/3)*I_n. In other words, we take enormous numbers of the size 10^16 or larger, which are accurate to at most 16 decimals, and add them so that the leading digits cancel, leaving no significant figures to approximate 1/3.
Theoretically, we could modify this algorithm to let the precision it uses grow with n, rather than use fixed precision. In this model, including the cost of the extra precise arithmetic, it is possible to show we can invert matrices accurately in O(log^2 n) time. But the overhead of such an algorithm makes it unattractive.
T = [ a(1) b(1) ]
[ c(1) a(2) b(2) ]
[ c(2) a(3) b(3) ]
[ .... .... .... ]
[ c(n-2) a(n-1) b(n-1) ]
[ c(n-1) a(n) ]
The solution via Gaussian elimination without pivoting would take 3 steps:
The parallel version of Gaussian elimination discussed in another section
would take O(n) steps to factorize, and O(n) steps for each triangular solve.
We will show how to use parallel prefix to do each of these in O( log n) steps.
Write T=L*U with
L = [ 1 ] and U = [ d(1) e(1) ]
[ l(1) 1 ] [ d(2) e(2) ]
[ l(2) 1 ] [ ... ... ]
[ ... ... ] [ d(n-1) e(n-1) ]
[ l(n-1) 1 ] [ d(n) ]
equating T(i,j) = (L*U)(i,j) for j=i-1, i, i+1 yields
(i,i-1): c(i-1) = l(i-1)*d(i-1)
(i,i): a(i) = l(i-1)*e(i-1) + d(i)
(i,i+1): b(i) = e(i)
Thus we may substitute b(i) for e(i). Solving the first equation for
l(i-1) and substituting in the second equation yields
d(i) = a(i) - e(i-1)*c(i-1)/d(i-1)
= a(i) + f(i)/d(i-1)
where f(i)=-e(i-1)*c(i-1). If we can solve this recurrence for all d(i)'s,
then we can compute all the l(i)=c(i)/d(i) in a single time step.
We will show how to use parallel prefix to evaluate this recurrence in log n time. Write d(i) = p(i)/q(i), and rewrite the recurrence as
p(i) a(i)*p(i-1) + f(i)*q(i-1)
---- = a(i) + f(i)/ ( p(i-1)/q(i-1) ) = -------------------------
q(i) p(i-1)
Now we set p(i) = a(i)*p(i-1) + f(i)*q(i-1) and q(i) = p(i-1), or
[ p(i) ] = [ a(i)*p(i-1) + f(i)*q(i-1) ] = [ a(i) f(i) ] * [ p(i-1) ]
[ q(i) ] [ p(i-1) ] [ 1 0 ] [ q(i-1) ]
= M(i) * [ p(i-1) ]
[ q(i-1) ]
= M(i) * M(i-1) * ... * M(1) * [ p(0) ] = N(i) * [ p(0) ]
[ q(0) ] [ q(0) ]
where f(1) = 0, p(0) = 1, and q(0) = 0. Thus, we need to compute the
prefix-products N(i) for i=1 to n, and this can be done using parallel
prefix with 2-by-2 matrix multiplication as the associative operation,
in O(log n) steps. Thus, we can LU factorize T=L*U in O(log n) steps.
Now we consider solving the triangular system U*x=z in O(log n) steps; solving L*z=y is analogous. We again convert to parallel-prefix with 2-by-2 matrix multiplication as the operation. Equating (U*x)(i) = z(i) yields
d(i)*x(i) + b(i)*x(i+1) = z(i)
and rearranging yields the recurrence
x(i) = (-b(i)/d(i)) * x(i+1) + (z(i)/d(i))
= alpha(i) * x(i+1) + beta(i)
which we want to solve for decreasing values of i. We reexpress this as
[ x(i) ] = [ alpha(i) * x(i+1) + beta(i) ]
[ 1 ] [ 1 ]
= [ alpha(i) beta(i) ] * [ x(i+1) ] = P(i) * [ x(i+1) ]
[ 0 1 ] [ 1 ] [ 1 ]
= P(i) * P(i+1) * ... * P(n-1) * [ x(n) ] = Q(i) * [ x(n) ]
[ 1 ] [ 1 ]
where x(n) = z(n)/d(n). Again, we can compute the "parallel suffixes" Q(i)
in O(log n) steps using 2-by-2 matrix multiplication.
This algorithm computes the same factorization that LU without pivoting would compute, and is therefore subject to at least the same instabilities as that algorithm.
Combining the techniques of this and the last section let us solve n-ny-n linear systems with bandwidth m in time O((log n)(log m)).
c(-1) = 0
for i=0 to n-1
c(i) = ( ( a(i) xor b(i) ) and c(i-1) ) or ( a(i) and b(i) )
s(i) = a(i) xor b(i) xor c(i-1)
endfor
s(n) = c(n-1)
The challenge is to propagate the c(i) from right to left quickly.
After this all the sum bits s(i) can be computed in a single time step.
For simplicity let p(i) = [a(i) xor b(i)] (the "propagate bit") and
g(i) = [a(i) and b(i)] (the "generate bit"), which reduces the recurrence
for the carry-bit to
c(i) = ( p(i) and c(i-1) ) or g(i)
We evaluate this recurrence using parallel prefix, where the
associative operation is 2-by-2 Boolean matrix multiply, in almost
the same way as we solved U*x=z:
[ c(i) ] = [ p(i) and c(i-1) or g(i) ]
[ T ] [ T ]
= [ p(i) g(i) ] * [ c(i-1) ] = C(i) * [ c(i-1) ]
[ F T ] [ T ] [ T ]
= C(i) * C(i-1) * ... * C(0) * [ c(-1) ]
[ T ]
where c(-1) = F. Boolean matrix multiplication is associative, because
and and or satisfy the same associative and distributive
laws as multiplication and addition.
This algorithm is also called carry look-ahead, is used in virtually every microprocessor to perform integer addition, and was known in a rudimentary form to Babbage in the 1800's.
Theorem. (Kung). Let z(i) be defined by the degree d rational recurrence z(i) = f_i( z(i-1) ) as described above. Then
In other words, parallel prefix with 2-by-2 matrix multiplication is necessary and sufficient to parallel all rational recurrences that can be parallelized.Proof. First consider the case d=1. This means each f_i(z) is of the form
a(i)*z + b(i)
f_i(z) = -------------
c(i)*z + d(i)
We use the same trick that we have used before: write
z(i-1) = p(i-1)/q(i-1), so
p(i) a(i)*z(i-1) + b(i) a(i)*p(i-1)/q(i-1) + b(i)
z(i) = f_i(z(i-1)) = ----- = ------------------ = -------------------------
q(i) c(i)*z(i-1) + d(i) c(i)*p(i-1)/q(i-1) + d(i)
a(i)*p(i-1) * b(i)*q(i-1)
= -------------------------
c(i)*p(i-1) * d(i)*q(i-1)
Now we rewrite this as
[ p(i) ] = [ a(i)*p(i-1) * b(i)*q(i-1) ] = [ a(i) b(i) ] * [ p(i-1) ]
[ q(i) ] [ c(i)*p(i-1) * d(i)*q(i-1) ] = [ c(i) d(i) ] [ p(i-1) ]
= M(i) * [ p(i-1) ] = M(i) * M(i-1) * ... * M(1) * [ p(0) ]
[ q(i-1) ] [ q(0) ]
= N(i) * [ p(0) ]
[ q(0) ]
We see that we can compute all N(n) in log n time, as desired.
Next, consider the case d>1. We want to show that evaluating z(n) takes time at least proportional to n. To do this we consider z(n) as a rational function of n, and ask what its degree is, in the same sense as the degree of f_i: if we write z(n) as a rational function of z(0), what is the maximum of the degrees of the numerator and denominator? It is easy to see that since d-th powers of polynomials occur in each f_i, the degree can increase by a factor of d at each step, so the degree of z(n) is at most d^n, and will equal d^n barring fortuitous cancellations.
Now suppose we evaluate z(n) in m parallel time steps. We will show that the degree of z(n) is at most 2^m. Thus, for z(n) to have the right degree, we will need 2^m >= d^n, or m >= n, since d >= 2. Thus we will need m >= n parallel time steps to evaluate z(n), so no parallel speedup is possible. To see that the degree of z(n) is at most 2^m after m time steps, we proceed by induction. After m=0 steps, z(0) has degree 1 = 2^0. Suppose we have degree 2^(m-1) after m-1 time steps. At the m-th step, we can add, subtract, multiply or divide two rational functions of degree at most 2^(m-1) to get z(n). It is easy to confirm that doing any one of these four rational operations on 2 rational functions can at most double the maximum degree. This completes the proof.
We emphasize that this theorem is true because we permit only addition, subtraction, multiplication and division to be used. If we permit other, transcendental operations, like square roots, exponentials, and logarithms, further speedup is possible. For example, consider evaluating the square root using Newton's method to find a positive root of g(x) = x^2 - a = 0. This yields the recurrence
x(i+1) = (x(i)^2 + a)/(2*x(i)) = f(x(i))
Since the degree of f(.) is 2, this commonly used recurrence
cannot be accelerated. However, let us change variables using the
decidedly transcendental transformation
exp(y(i)) + exp(-y(i))
x(i) = sqrt(a) * coth(y(i)) = sqrt(a) * ----------------------
exp(y(i)) - exp(-y(i))
Then the recurrence becomes
y(i+1) = 2*y(i)
which has the trivial solution y(infinity) = infinity, whence
x(infinity) = sqrt(a) * coth(infinity) = sqrt(a) as expected.