CS267: Lecture 3, Jan 23 1996
Table of Contents
We studied how to write a fast matrix-multiplication algorithm on an abstract
machine with a 2-level memory hierarchy,
and then on the RS6000/590.
We did this in order to illustrate several more general points:
This explains our detailed look at the RS6000 architecture. We will not
look at other architectures in nearly as much detail, but just at those
parts which help us write good parallel code.
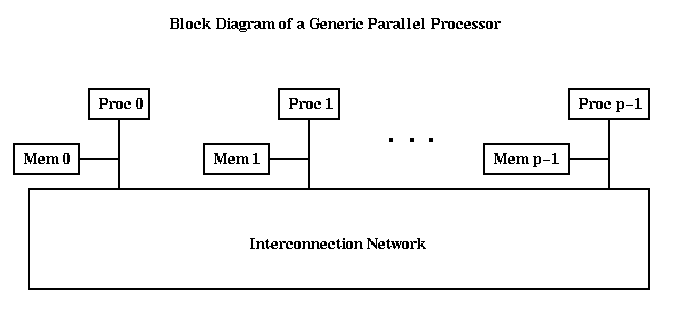
A block diagram of a "generic parallel computer" with p processors
is shown below. We will expand on this basic picture as time goes on, but
for now imagine each processor Proc_i executing some program, sometimes
referring to data stored in its own memory Mem_i, and sometimes communicating
with other processors over the Interconnection Network. This picture is
sufficiently abstract to include the case where the entire parallel computer
resides in one "processor" (as is the case with the dual floating point units
in the
RS6000/590)
where the parallel computer sits in one room
(the
IBM SP-2
-- which consists of multiple RS6000s -- or most other commercial
parallel computers), or where the parallel computer consists of computers
spread across continents, and the interconnection network is the
Internet, telephone system, or some other network.
There are three standard functions any parallel architecture must
provide. We will discuss particular implementations of these functions
later.
- Parallelism, or getting processor to work simultaneously.
- Interprocessor communication, or having processors exchange information.
- Synchronization, such as getting processors to ``agree'' on the value
of a variable, or a time at which to start or stop.
A programming model is the interface provided to the user by the
programming language, compiler, libraries, run-time system, or
anything else that the user directly "programs". Not surprisingly,
any programming model must provide a way for the user to express
parallelism, communication, and synchronization in his or her algorithm.
Historically, people usually designed a parallel architecture,
and then a programming model to match it. In other words,
the programming model expressed parallelism, communication
and synchronization in a way closely tied to the details
of the architecture. As a result, when the machine became
obsolete and new ones were built, all the programs written
for it became obsolete as well, and users had to start from
scratch. This did not exactly encourage widespread
adoption of parallel programming.
In the meantime, people have realized that it is possible and
valuable to build programming models independently of
architectures, to let people build up useful bodies of software
that survive generations of machine architectures. This implies
that we will view the systems we program as consisting of
layers, with the programming model at the top,
the machine at the bottom, and the compiler, libraries, and so
on providing a mapping from the programming model to the
machine, that hides machine details.
For example,
Connection Machine Fortran (CMF)
was orginally designed
for the Thinking Machines CM-2, and provided a programming model (called
data parallelism below) closely suited to the CM-2 architecture.
In particular, the CM-2 essentially required every processor to execute the
same instruction at the same time, a very limited form of
parallelism (called SIMD below). The next generation
CM5 was
later designed to permit much more flexible parallelism (called MIMD
below), but the CMF compiler was modified to continue to run CMF programs
on the new architecture.
So the programming model provided to the user (CMF) remained the same,
but the mapping to the machine (the way the compiler generated code)
changed significantly.
So the great benefit one gets for separating machines from programming
models is the ability to write programs that run portably across
several machines. The potential drawback is loss of performance,
depending on how well the programming model can be mapped to a
particular architecture. Not all programming models map equally
well to all architectures, and there are many hard research
questions left on to best implement these mappings.
Therefore, existing compilers, libraries, and run-time systems
are often incomplete, buggy, inefficient, or some combination of the
three. Caveat programmor. When we study programming models
later, we will spend some of our time on how these mappings work,
so we can predict whether one parallel program is more efficient
than another one for solving the same problem.
The following sections are organized as follows.
First, we will discuss some standard ways in which
parallel architectures provide parallelism, communication,
and synchronization.
Second, we will very briefly do the same for our
programming models, pointing out how the programming models
have "natural" architectures for which they were originally
developed, even though they can be mapped to others.
Subsequent lectures will look at these programming models
in great detail.
Third, we will present standard ways to measure the
performance of parallel programs.
Finally, we will discuss a set of sample applications called
Sharks and Fish,
that we will use to illustrate all these programming models.
Parallelism
The two main styles of parallelism are SIMD and MIMD, or
single-instruction-multiple-data and
multiple-instruction-multiple-data.
This is old terminology, dating to
Flynn's taxonomy of parallel machines in the 1960s.
SIMD means performing the same operation (e.g. single instruction)
on multiple pieces of data in parallel, and MIMD means performing
arbitrary operations (e.g. multiple instructions) on different data
at the same time. In the SIMD case, one can think of the generic
parallel processor in the figure above as being augmented by another control
processor, which at every cycle sends a common instruction
to each Proc_i to execute. Examples of SIMD parallelism
include the vector operations on a single processor
Cray T-90 and earlier
Cray vector machines; the Thinking Machines CM-2; and a single
pipelined floating point unit in the RS6000/590, where the
adder and multiplier must operate in a pipeline controlled by a
single fused-multipy-add instruction.
Examples of MIMD parallelism include almost every commercial
parallel machine, where each processor may also be programmed
as a standard sequential machine, running sequential jobs.
Note that a particular machine can exhibit both SIMD and MIMD
parallelism at different levels, such as a multiprocessor
Cray T90. MIMD parallel is more flexible and more common than
SIMD parallelism, which now usually appears within individual
floating point or memory units.
Communication
In order to discuss communication, we must first discuss
how an architecture names the different memory locations
to which instructions must refer. Neither humans nor machines
can communicate without a common set of names upon which they
agree. Recall that the memory of a conventional (nonparallel)
computer consists of a sequence of words, each of
which is named by its unique address, an integer.
A typical computer instruction will look like "load r1, 37",
which says to load the word stored at memory address 37 into
register r1. Examining the figure of a generic parallel computer
above, we see that there are multiple memories Mem_i.
The two major ways to name the memory locations of these
multiple memories are called shared memory and
distributed memory. With shared memory, each word
in each memory has a unique address which all processors
agree on. Therefore, if Proc_1 and Proc_3 both execute
the instruction "load r1, 37", the same data from one
location in one Mem_i will be fetched into register r1 of
Proc_1 and register r1 of Proc_3. With distributed memory,
Proc_1 would fetch location 37 of Mem_1 and Proc_3 would fetch
location 37 of Mem_3. Therefore, to communicate on a shared
memory machine, Proc_1 and Proc_3 merely need to load and
store into a common address, such as 37. On a distributed
memory machine, explicit messages must be sent over
the communication network, and be processed differently than
simple loads and stores.
On the market one can find both
successful shared memory machines
(click here
for examples)
and successful distributed memory machines
(e.g.
IBM SP-2,
Intel Paragon,
along with networks of workstations).
Roughly speaking, shared memory machines
offer faster communication than distributed memory
machines, and they naturally support a programming
model (also called shared memory) which is
often easier to program than the programming model
natural to distributed memory machines (called
message passing).
However, shared memory machines are harder to build
(or at least more expensive per processor) than distributed
memory machines, for large numbers of processors
(more than 32, say, although this number is growing).
An important property of communication is its cost, which
is essential to understanding the performance of a parallel program.
Suppose we want to send n words of data from one processor to another.
The simplest model that we will use for the time required by this
operation is
time to send n words = latency + n/bandwidth
We consider sending n words at a time because on most machines
the memory hierarchy dictates that it is most efficient to
send groups of adjacent words (such as a cache line) all at once.
Latency (in units of seconds) measure the time to send an
"empty" message. Bandwidth (in units of words/second) measures
the rate at which words pass through the interconnection network.
The form of this formula should be familiar: recall that the time to
process n words by a pipeline of s stages, each stage taking t seconds, is
(s-1)*t + n*t = latency + n/bandwidth
Thus, the intercommunication network works like a pipeline,
"pumping" data through it at a rate given by bandwidth,
and with a delay given by the latency for the first word
in the message to make it across the network.
To give an order-of-magnitude feeling for the cost of communication,
let us change units to measure latency and bandwidth in cycles
and words per cycle, respectively. Recall that a cycle in the basic
unit of time in which a computer does one operation, such as an add.
On shared memory machines, where communication is fastest, latency
may be hundreds of cycles. At the other extreme,
a distributed memory machine consisting of
a network of workstations running PVM over an Ethernet,
latency may be O(10^5) cycles (this includes both hardware and software delays).
In other words, in one communication
the processor could instead of done anywhere from 10^2 to 10^5
other useful operations. The time per word (reciprocal of bandwidth)
is typically much lower than the latency (O(10) to O(1000) MBytes/second),
so it is often much more efficient to send one large message than
many small one. We will see that the difference between a good parallel
algorithm and a bad one is often the amount of communication they perform.
Some shared memory machines are constructed out of clusters
of smaller shared memory machines. In this case, it is often
faster to access memory located with the cluster, than
memory in another cluster. Such machines are called NUMA machines,
for NonUniform Memory Access, and require (at least) two
latencies and two bandwidths (for nearby and remote memory)
to model communication accurately.
We will expand on this simple model later in
Lecture 9.
Synchronization
Synchronization refers to the need for two or more
processors to agree on a time or a value of some data.
The three most common manifestations of synchronization
(or lack of it) are
mutual exclusion, barriers, and memory consistency.
We discuss each briefly.
Mutual exclusion refers permitting just one processor
access to a particular memory location at a time.
To illustrate the need for such a facility, suppose we want
to compute the sum s of p numbers x_i, where Proc_i has
computed x_i. The "obvious" algorithm is for each processor
to fetch s from the processor that owns it (say Proc_0),
add x_i to s, and store s back in Proc_0.
Depending on the order in which each processor accesses s on
Proc_0, the answer could range from the true sum to any
partial sum of the x_i. For example, suppose that we
only want to add x_1 and x_2. Here are two unintended possibilities
for the execution (the time axis is vertical, and we indicate
the time at which each processor executes each instruction.
Proc_1 Proc_2
| load s (=0)
| fetch s (=0)
| s = s+x_1 (=x_1) s=s+x_2 (=x_2)
| store s (=x_1)
| store s (=x_2)
V
time
The loads and stores of s involve communication with Proc_0.
The final value of s stored in Proc_0 is x_2, since this
is the last value stored in s. If the two stores are reverse
in time, the final value of s would be x_1.
This is called a race condition, because the final
value of s depends on the nondeterministic condition of whether
Proc_1 or Proc_2 is slightly ahead of the other.
Mutual exclusion provide a mechanism to avoid race conditions,
by allowing just one processor exclusive access to a variable.
This is often implemented by providing a "test&set" instruction,
which sets a particular word to a particular value, while fetching
the old value, all without other processors being able to
interfere. Later when we discuss programming models we will
show how to solve the problem of adding numbers using the
test&set instruction.
Barriers involve each processor waiting at the same point in
the program for all the others to "catch up", before proceeding.
This is necessary to make sure a parallel job on which all the
processor had been cooperating is indeed finished. Barrier can
be implemented in software using the test&set instruction above,
but some architectures (like the CM-5) have special hardware for this.
Memory consistency refers to a problem
on shared memory machines with caches. Suppose processors Proc_1 and
Proc_2 both read memory location 37 into their caches. The purpose
of caches is to eliminate the need to access slow memory when accessing
commonly used data, like location 37. After reading and using location
37, suppose Proc_1 and Proc_2 then try to store new, different values
into it.
How will the differing views of memory held by Proc_1 and Proc_2 be
reconciled? Which value will eventually make it back into main memory
at location 37? Insisting that each processor have the same view of
all memory locations at the same time, so that location 37 has a
single value across the machine, seems very reasonable.
This is called sequential memory consistency,
because it is the same way memory looks on a sequential machine.
But it is expensive to implement, because all writes must hit main
memory, and update all other caches in the machine rather than
just update the local cache. This expense has led some shared memory
machine to offer weak(er) memory consistency models, which
leave it to the user to program in such a way that these problems
cannot occur. We discuss this later when we discuss programming models.
We give a very brief overview of our 4 major programming models for this course,
how they let the user express
parallelism, communication and synchronization, and how they map to
particular architectures. Subsequence lectures will discuss these models
in great detail.
Data Parallelism
Data parallelism means applying the same operation, of set of operations,
to all the elements of a data structure. This model evolved historically from
SIMD architectures. The simplest examples are array operations like
C = A+B, where A, B and C are arrays, and each each entry may be added in parallel.
Data parallelism generalizes to more complex operations like global sums, and to
more complex data structure like linked lists. Communication is implicit,
meaning that if a statement like C=A+B requires communication, because elements of
the arrays A, B and C are stored on different processors, this is done invisibly
for the user. Synchronization is also implicit, since each statement completes
execution before the next one begins. Our main data parallel programming language
will be
Connection Machine Fortran (or CM Fortran, or simply CMF).
A CMF manual is
available in Volume 2 of the class
reference material, or by typing cmview while logged in to rodin.
CMF is quite similar to the more recently emerging standard
High Performance Fortran, or HPF,
which many manufacturers are supporting.
We will use the sequential programming
language
Matlab
(which runs on all workstations across campus) to prototype
data-parallel codes, since it many similar to CMF in many ways.
In addition to Matlab's own on-line
help facility, a mini-manual is located in Volume 4 of the class
reference material, or
here.
The recent sequential language
Fortran 90
updates Fortran 77 to have similar array operations, as well
as recursion, structures, limited pointers, and other more modern
programming language features.
Message Passing
Message Passing means running p independent sequential programs,
written in sequential languages like C or Fortran, and communicating by
calling subroutines like send(data,destination_proc) and
receive(data,source_proc) to send data from one processor
(source_proc) to another (destination_proc).
In addition to send and
receive, there are usually subroutines for computing global sums,
barrier synchronization, etc. Since it is inconvenient to maintain
p different program texts for p processors (since p will vary from machine
to machine), there is usually a single program text executing on all
processors. But since the program can branch based on the processor number
(MY_PROC) of the processor on which it executes,
if (MY_PROC = 0) then
call subroutine0
elseif (MY_PROC = 1) then
call subroutine1
...
different processors can run completely independently.
This is called SPMD programming (single program multiple data).
This programming model is natural for
MIMD distributed memory machines, and is
supported on the CM-5 in the message-passing library
CMMD (not really an acronym). See Volume 1 of the
class reference material
for documentation.
Two similar but more portable message passing libraries are
PVM and
MPI.
Message-passing is
the "assembly language programming" of parallel computing, often resulting
in long, complicated, and error-prone programs. But it is also the
most portable, since PVM and MPI do run (or will run) on all almost
all platforms.
Shared memory programming with threads
Shared memory programming with threads is a natural programming
model for shared memory machines. There is a single program text, which
initially starts executing on one processor. This program may execute
a statment like "spawn(proc,0)", which will cause some other processor
to execute subroutine proc with argument 0. Subroutine proc can "see"
all the variables it can normally see according to the scoping rules of
the serial language. The main program which spawned proc can later
wait for proc to finish with a barrier statement, go on to spawn other
parallel subroutine calls, etc. We will use two such programming models
this semester. The first is C augmented with
Solaris threads, running on a Sparc multiprocessor.
The second is
pSather,
a parallel object oriented language designed and
implemented locally at ICSI .
A manual is also located in Volume 4 of the class
reference material.
Split-C
Split-C is a locally designed and implemented language which
augments C with just enough parallel constructs to expose the basic
parallelism provided by the machine. It includes features of data parallelism,
message passing, and shared memory.
Originally implemented for the CM-5, it has been ported to many machines,
including all the platforms we will use this semester.
A manual is located in Volume 4 of the class
reference material.
In addition to the major programming languages listed above, we will
mention other languages, libraries and run-time systems throughout the course.
The following is a list of ways we will use to measure the performance of
a parallel program. We will use these criteria to measure the difference
between a good parallel program and a bad one, or
(See also section 4.1 of the book by Kumar et al, or click
here for a gentler introduction.
Throughout these notes we will use p to denote the number of parallel
processors available, and n to denote the problem size. For example,
in the case of matrix multiplication, n may denote the dimension of the
matrix. It would also be reasonable to measure problem size by the
amount of input data, which would be the square of the matrix dimension
for matrix multiplication.
So it is important to be specific when defining n.
Speedup and efficiency are the most common ways to report the performance
of a parallel algorithm
It is a ``pseudo theorem'' that Speedup(p) <= p, or
Efficiency(p) <= 1, because in principle one processor can simulate
the actions of p processors in at most p times as much time,
by taking one step of each of the p serial programs making up the
parallel
program, in a round robin fashion. This idea is due to Brent.
Actually, we can sometimes get "superlinear speedup", i.e.
Speedup(p)>p, if either
Our pseudo-theorem implies that if we plot the straight line "Speedup(p)=p"
through the
origin on a speedup plot, this will bound the true speedup from above,
and the quality of the parallel implementation can be measured by how
close our algorithm gets to this ``perfect speedup curve''.
Perfect speedup is seldom attainable. Instead, we often
try to design "scalable algorithms", where Efficiency(p) is bounded away
from 0 as p grows. This means that we are guaranteed to get some benefit
proportional to the size of the machine, as we use more and more processors.
A common variation on these performance measures is as follows:
Since people often buy
a larger machine to run a larger problem, not just the same problem
faster, we let problem size n(p) grow with p, to measure the
``scaled speedup''
T(1,n(p))/T(p,n(p)) and ``scaled efficiency'' T(1,n(p))/(T(p,n(p))*p).
For example, we may let n(p) grow so that the amount of memory used
be a constant per processor, no matter what p is. In the case
of matrix multiplication C = A*B, this means the the matrix dimension N
for p processors would satisfy 3*N^2 = n(p) = p*M, where M is the amount
of memory used per processor.
Amdahl's law gives a simple bound on how much speedup we can expect:
suppose a problem spends fraction f<1 of its time doing
work than can be parallelized, and fraction s=1-f doing serial work,
which cannot be parallelized. Then T(p) = T(1)*f/p + T(1)*s, and
Speedup(p) = T(1)/T(p) = 1/(f/p+s) <= 1/s, no matter how big p is.
Efficiency(p) = 1/(f+s*p) goes to 0 as p increases.
In other words, speedup is bounded by 1/s, and in fact increasing p past s/f can't
increase speed by more than a factor of two.
Amdahl's law teaches us this lesson:
We need to make sure there are no serial bottleneck (the s part)
in codes if we hope to have a scalable algorithm.
For example, even if only s=1% of a program is serial, the speedup is
limited to 100, and so it is not worth using a machine with more than
100 processors. As we will see,
this means we need to measure performance carefully (profiling) to
identify serial bottlenecks.
The assignments will discuss how to profile programs accurately.
This is a collection of 6 successively more difficult parallel programming
problems, designed to illustrate many parallel programming problems
and techniques. It is basically a simulation of "particles" moving around
and interacting subject to certain rules, which are not entirely
physical but instructive and amusing.
Some of the problems are discrete
(the sharks and fish can only occupy a discrete set of positions), and
some are continuous (the sharks and fish can be anywhere).
We have working implementations of many of these problem in 6
programming models, 5 of which are parallel, to illustrate
different ways the same algorithm is expressed in different parallel
programming models. You will have programming assignments involving modifying
some of these implementations. The 6 languages are
An outline of the rules followed by all 6 sharks and fish problems
is as follows.
Here are the rules for the 6 different sharks and fish problems in brief,
with more details available here.
The following software for these problems exists.
It can be seen by
clicking on the x's below. In each case you will see a directory
of source code for each problem. In the case of the Matlab code,
the routine fishXinit.m is an initialization program, to be run
first to set up the problem (where X varies from 1 to 5),
and fishX.m is the main Matlab solution routine.
Language Problem number
1 2 3 4 5 6
Matlab x x x x x
CMMD x x x
CMF x x x x
Split-C x x x x
Sun Threads x x
pSather x x x

