We will use Matlab notation to express our algorithms below. Recall that
The 6 most basic problem of linear algebra are summarized below. For details, see any good text book in numerical linear algebra ... In a future lecture we will give examples of where they arise in real physical applications.
After a summary of general computational aspects of these problems, we will discuss solving problem 1, Ax=b, using Gaussian elimination.The most important determiner of which algorithm to use for these problems is whether the matrix A is dense or sparse. A dense matrix has all (or mostly) nonzero entries, without any special properties that would let one represent it in much less than n^2 words. Sparse matrices are the complement of dense matrices, either with lots of zero entries, or otherwise much more compactly representable than n^2 words. The algorithms for sparse matrices, which are very common in science and engineering, are often rather different than algorithms for dense matrices, and we will discuss them in detail later. For a small example click here. The first picture is a mesh around a wing. The physical problem is to compute the airflow around the wing at the mesh points. This leads to solving a sparse n-by-n system of spd linear equations Ax=b, where n=4253 and A has the "sparsity structure" in the top left plot of the second picture (black dots represent nonzero entries, the rest are zero). Only .16% of the 4253^2 entries of A are nonzero. The top right plot of the second picture is a different view of the matrix, with the rows and columns permuted. If we did Gaussian elimination on the spd matrix A without taking sparsity into account, it would take (1/3)*n^3 = 2.6e10 floating point operations. If we do Gaussian elimination on the matrix in the top left, and take sparsity into account by not doing unnecessary operations on zero entries, it does over 2200 times fewer operations, resulting in the Cholesky factor at the bottom left. If we do Gaussian elimination on the matrix at the top right, we get the Cholesky factor at the bottom right for 4 times fewer operations still. This matrix is available in matlab by typing demo, and clicking on continue/Matlab_Visit/Matrices/Select_a_demo/Cmd_Line_Demos/NASA_Airfoil; all the pictures and other manipulations are one-liners in matlab. Designing and implementing parallel sparse matrix algorithms is a currently active field of research, and at least one project is available in this area. LAPACK and ScaLAPACK currently deal mostly with dense matrices.
(Temporary pointer to nested dissection illustration)
The next important distinction is between the first three problems (solving Ax=b and least squares problems), and the last three problems (eigenvalues and the SVD). The first three problems have exact, finite solution procedures, and the latter three can only be solved approximately. The first three problems have exact finite solutions in the sense that O(n^3) algorithms exist for each, which would yield the exact solution in the absence of round-off errors. (Analyzing roundoff is a topic for a numerical analysis class, and we will only mention it here when it requires us to modify the algorithm to make it reliable.) In contrast, the second three problems only have iterative solutions (for 5x5 matrices or larger), because they implicitly require finding the roots of the characteristic polynomial of the matrix A: p(x)=determinant(A-x*I) (for the SVD substitute A'*A for A). As shown by Galois, no finite algorithm can exist to find the roots of a general polynomial of degree 5 or greater. A large variety of iterative solutions exist. In practice, the best iterations converge so reliably and so rapidly (quadratically or cubically) that they are often considered to be finite solutions.
The latter three problems are all solved in 2 phases: a (finite) algorithm to reduce the original dense matrix to a more compactly representable form with the same eigenvalues (or singular values), and an iterative phase on the compact form. We will again distinguish the first three problems from the initial phases of the second three problems: For the first three problems, it is known how to do almost all the work by using matrix-matrix multiplication (BLAS3). In contrast, the first phases of the second three problems are more difficult to convert to BLAS3. The algorithm in LAPACK does 50% BLAS3 and 50% matrix-vector multiplication (BLAS2). multiplication. More recently, work on "multi-step band-reduction" by C. Bischof, X. Sun, and others has shown that if no eigenvectors are desired, one can use nearly 100% BLAS3. If eigenvectors are desired, one either has to use BLAS2 or increase the operation count significantly (by 2n^3).
In other words, we can in principle take nearly full advantage of the memory hierarchy for the first three problems, but not the second three, at least if eigenvectors are desired and we do not want to increase the operation count significantly.
Now consider just the last three problems. The iterative phase of finding the eigenvalues of a general matrix is much more expensive than the initial reduction phase. In contrast, the best recent iterations for the symmetric eigenvalue problem and SVD are in principle much cheaper than the corresponding reduction phases (this was not true until recently).
Good parallel software for the first three problems exists in LAPACK and ScaLAPACK. Software for the second three problems exists in LAPACK, with recent better algorithms on the way. ScaLAPACK currently only solves one of the second three problems (the symmetric eigenproblem), and the Feb 1995 release makes certain unfortunate compromises between parallel efficiency and accuracy, which better algorithms should make unnecessary. Class projects to improve and expand ScaLAPACK are available.
It is interesting to ask whether the best parallel algorithm is always a parallel version of the best serial algorithm. This is usually the case, and in fact the search for better parallel algorithms has sometimes led to better serial algorithms as well. However, there are some interesting exceptions. For example, certain "banded" linear systems can be solved more quickly using parallel-prefix than Gaussian elimination, but the results are numerically unstable in the presense of roundoff, and so potentially much less accurate. Currently, LAPACK and ScaLAPACK use different algorithms for finding eigenvalues, but we expect them to use the same algorithm eventually, once we better understand the problem.
for i = 1 to n-1 ... for each column i, zero it out below the diagonal
for j = i+1 to n ... each row j below row i
for k = i to n ... add a multiple of row i to row j
A(j,k) = A(j,k) - (A(j,i)/A(i,i)) * A(i,k)
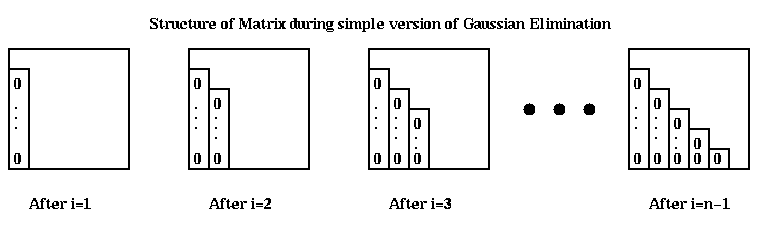
Let us improve this rudimentary implementation step by step. First, we remove the constant (A(j,i)/A(i,i)) from the innermost loop:
for i = 1 to n-1
for j = i+1 to n
m = A(j,i)/A(i,i)
for k = i to n
A(j,k) = A(j,k) - m * A(i,k)
Next, we avoid computing results we know, i.e. the zeros below the diagonal:
for i = 1 to n-1
for j = i+1 to n
m = A(j,i)/A(i,i)
for k = i+1 to n
A(j,k) = A(j,k) - m * A(i,k)
It will be convenient to store the multipliers m in the implicitly created
zeros below the diagonal, so we can use them later to transform the right
hand side b:
for i = 1 to n-1
for j = i+1 to n
A(j,i) = A(j,i)/A(i,i)
for j = i+1 to n
for k = i+1 to n
A(j,k) = A(j,k) - A(j,i) * A(i,k)
Now we use Matlab notation to express the algorithm even more compactly.
Note that the last two loops are really multiplying the column vector
A(i+1:n, i) times the row vector A(i, i+1:n), and add the resulting
(n-i)-by-(n-i) matrix to A(i+1:n, i+1:n):
for i = 1 to n-1
A(i+1:n, i) = A(i+1:n, i) / A(i,i)
A(i+1:n, i+1:n) = A(i+1:n, i+1:n) - A(i+1:n, i)*A(i, i+1:n)
Thus, the inner loop consists of one BLAS1 operation (scaling
A(i+1:n,i) by a constant), and one BLAS2 operation (adding a rank-one matrix
-A(i+1:n,i)*A(i,i+1:n), to A(i+1:n, i+1:n)).
Here is a picture of what happens at step i.
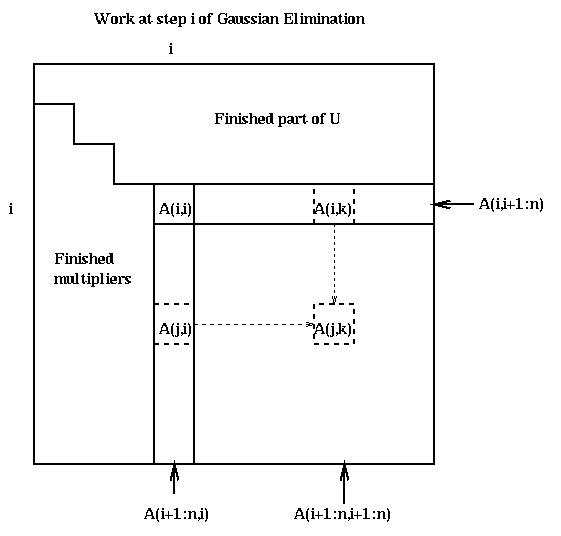
Call the strictly lower triangular matrix of multipliers which is stored below the diagonal of A after the algorithm ends M, and let L=I+M. We state the following easy lemma without proof.
Lemma. (LU Factorization). If the above algorithm terminates (i.e. it did not try to divide by zero) then A = L*U.
Now we can state our complete algorithm for solving A*x=b:
1) Factorize A = L*U. 2) Solve L*y = b for y by doing forward substitution. 3) Solve U*x = y for x by doing backward substitution.Then x is the solution we seek because A*x = L*(U*x) = L*y = b.
Let us compute the serial and PRAM complexity of this algorithm. From the matlab code, it is easy to see that the number of floating point operations performed (serial complexity) is
sum_{i=1}^{n-1} [ (n-i) ... cost of A(i+1:n,i+1:n)/A(i,i)
+ 2*(n-i)^2 ] ... cost of A(i+1:n,i+1:n)-A(i+1:n,i)*A(i,i+1:n)
= (2/3)*n^3 + O(n^2)
Solving L*y=b and U*x=b each only cost n^2, so the total cost is
still (2/3)*n^3 + O(n^2).
Assuming we have one processor per matrix entry, and that communication is free (the PRAM model), the cost is
sum_{i=1}^{n-1} [ 1 ... cost of A(i+1:n,i+1:n)/A(i,i)
+ 2 ] ... cost of A(i+1:n,i+1:n)-A(i+1:n,i)*A(i,i+1:n)
= 3*(n-1)
since all the divisions in the inner loop can be done at once,
all the multiplications can be done at once, and all the subtractions
can be done at once. Thus, a lot of parallelism is available
in this algorithm for us to exploit. One can also confirm that solving
L*y=b and U*x = y in straightforward ways:
y(1:n) = b(1:n) ... in practice, y is overwritten on b
for i = 1 to n-1
y(i+1:n) = y(i+1:n) - y(i)*L(i+1:n,i)
x(1:n) = y(1:n) ... in practice, x is overwritten on y, i.e. b
for i = n downto 1
x(i) = x(i)/U(i,i)
x(1:i-1) = x(1:i-1) - x(i)*U(1:i-1,i)
costs (1+2*(n-1)) + (1+n+2*(n-1)) = 5n-2, for a grand total of 8*n-5.
Interestingly, in the PRAM model, solving triangular systems with the
most straigthtforward algorithms is about as expensive as LU factorization,
whereas triangular system solving was much cheaper on a serial machine.
Here are some obvious problems with this algorithm, which we need to address:
In the next lecture we will address both these issues.