Most of these lies are "little white lies" that don't matter too much since, 1/3 and .3333333333333333 (16 digitis) are close enough together for most purposes.
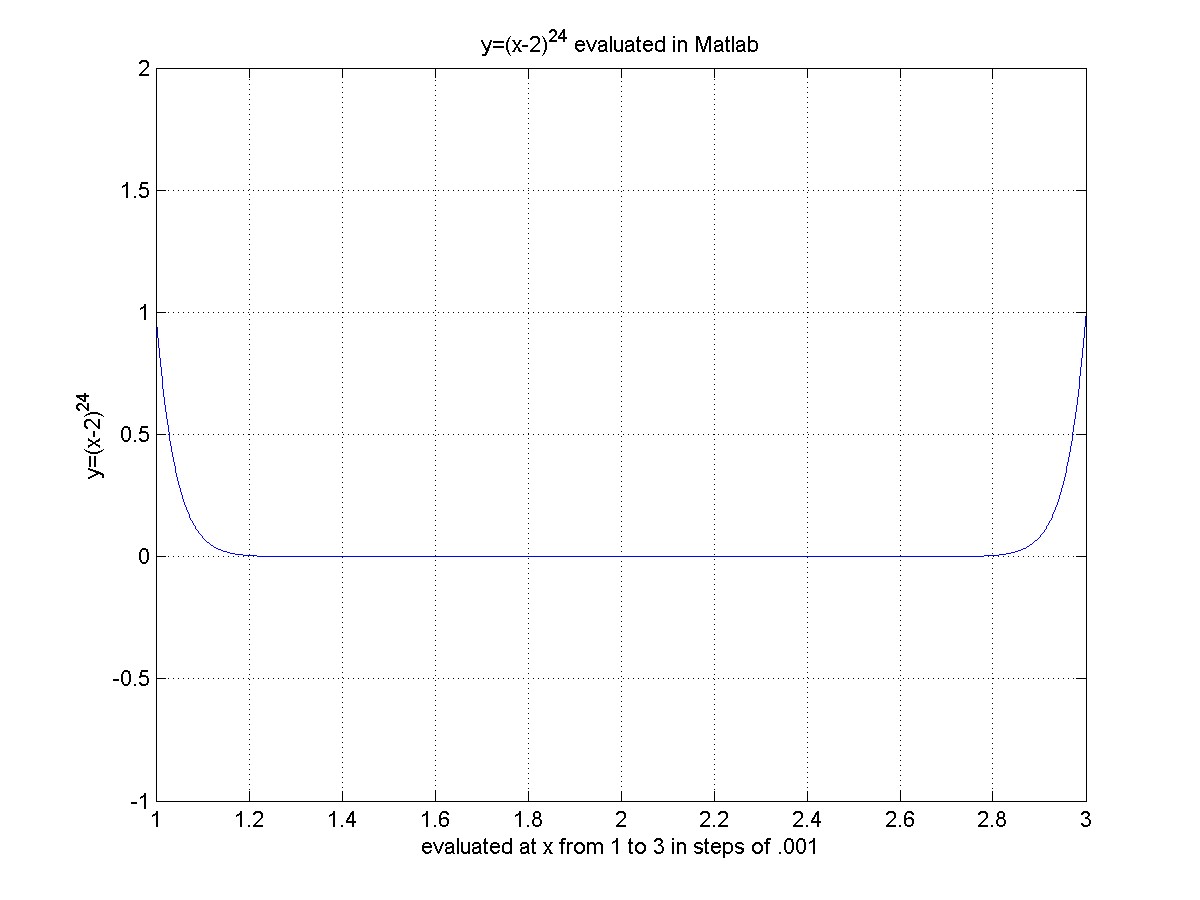
But sometimes these "little white lies" can add up to a much bigger lie. For example consider the polynomial y=(x-2)^(24), whose correct graph is shown below in the range 1 <= x <= 3. For most values of x in this range, y is very small, so the graph looks like it is sitting on y=0, whereas the true answer is just very tiny. For example (2.5 - 2)^(24) is about 6 x 10^(-8).

But now suppose we evaluate the mathematically identical polynomial
that we get from multiplying out (x-2)^(24):
y = (x-2)^(24)
= x^(24) - 48*x^(23) + 1104*x^(22) -16192*x^(21) + 170016*x^(20) - 1360128*x^(19) + 8614144*x^(18) - 44301312*x^(17) + 188280576*x^(16) - 669442048*x^(15) + 2008326144*x^(14) - 5112102912*x^(13) + 11076222976*x^(12) - 20448411648*x^(11) + 32133218304*x^(10) - 42844291072*x^9 + 48199827456*x^8 - 45364543488*x^7 + 35283533824*x^6 - 22284337152*x^5 + 11142168576*x^4 - 4244635648*x^3 + 1157627904*x^2 - 201326592*x + 16777216.
We should get the same plot, since the two polynomials are mathematically
identical. But the computer gives us the following picture:
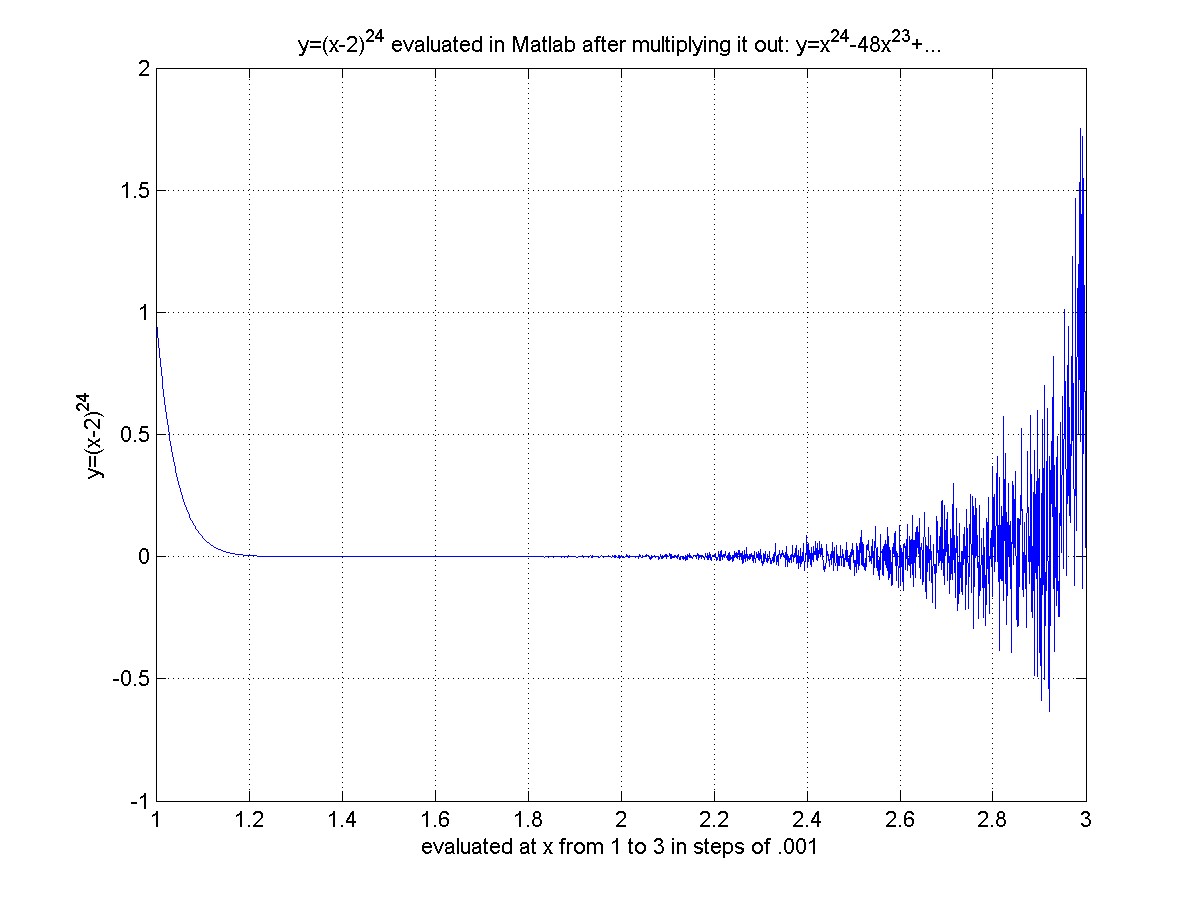
You can see that these two plots differ drastically, even though they should be the same, all because those "little white lies," also called "roundoff errors," can sometimes add up and be larger than you might think.
The point of this example is that only if you know enough calculus to know what kind of graph to expect, would you be able to immediately recognize that the second plot is nonsense, and you have to do something different (evaluate a different expression, or use more digits of precision).
(1) Will our lecture hall collapse in an earthquake? Engineers and architects use computers to solve differential equations that say whether a proposed building design will stand or collapse during various types of earthquakes. Your life could depend on whether these programs are getting the right answer.
(2) Is climate change really caused by people, so that only by changing how people live and use energy can we hope to ameliorate its effects? This is a huge question, and teams of climate modellers around the world are constantly working to improve the ability of their programs to solve the differential equations that predict climate in the future. A lot of the uncertainty in these predictions come from using models that are too simple, or having too little accurate measured data to use, as well as the roundoff errors mentioned above. But a lot of our future may depend on solving these equations accurately.
Let me mention one more, with a Berkeley connection:
(3) Can we trust the Nation's nuclear weapons not to blow up by mistake? Before 1992, when the President decided to stop nuclear testing, we would occasionally explode one to make sure it worked properly. Since then, the country has had to rely in part on solving the differential equations that describe the nuclear reactions in a nuclear bomb to make sure it behaves as expected. For more details, click here.
The Berkeley connection is that the scientific director of the Manhattan Project which built the first nuclear weapon, was J. Robert Oppenheimer, a Berkeley physics professor. The University of California is still partly responsible for managing the Nation's nuclear weapons laboratories.
The largest computers in the world (that we know about publicly) have usually been used by these nuclear weapons laboratories. For a list of the 500 largest computers in the world (updated biannually), click here. As of Sept 2008, the two largest computers in the world were at these weapons labs. On the other hand, the most common application area in which these 500 computers were used was finance (about 15% of them).