
Recent Awards:
Jack Dongarra was recently named an IEEE Fellow for "contributions and leadership in the field of computational mathematics."
The NetSolve and ATLAS projects both won R&D 100 Awards for 1999.
James Demmel and Mark Adams received the Karl Benz Award for the best industrial application, ``Parallel Unstructured Multigrid Finite Element Solvers,'' in Mannheim SuParCup '99 at Mannheim Supercomputer '99 Conference, June 10-12, 1999
NetSolve
Overview:
NetSolve is a client-server system enabling users to solve complex scientific problem remotely. The system allows users to access both hardware and software computational resources distributed across a network. NetSolve searches for computational resources on a network, chooses the best one available, and using retry for fault-tolerance solves a problem, and returns the answers to the user. A load-balancing policy is used by the NetSolve system to ensure good performance by enabling the system to use the computational resources available as efficiently as possible. Our framework is based on the premise that distributed computations involve resources, processes, data, and users, and that secure yet flexible mechanisms for cooperation and communication between these entities is the key to metacomputing infrastructures.
Some goals of the NetSolve project are:
Interfaces in Fortran, C, Matlab, and Java have been designed and implemented which enable users to access and use NetSolve more easily. An agent-based design has been implemented to ensure efficient use of system resources.
One of the key characteristics of any software system is versatility. In order to ensure the success of NetSolve, the system has been designed to incorporate any piece of software with relative ease. There are no restrictions on the type of software that can be integrated into the system.
Results and Interactions:
Currently, a wide range of applications have been integrated and make use of the NetSolve system. Here, we identify a few of these applications and summarize how they have taken advantage of NetSolve.
See NetSolve Application for more details.
NetSolve has integrated numerous systems (either in part or in whole) to help in its functionality. Here we make mention of these systems and summarize what components we have integrated and the reasons for doing so.
In addition NetSolve has been extended to enable software from the following DOE2000 software packages: LAPACK, ScaLAPACK, SuperLU, PETSc, and AZTEC.
There have been many enhancements and additions made to the NetSolve project over the past year. The majority of these new features will be distributed as a part of the NetSolve 1.3 release slated for March of this year. Below, we list and briefly describe these enhancements:
Plans:
Overview:
ATLAS is an approach for the automatic generation and optimization of numerical software for processors with deep memory hierarchies and pipelined functional units. The production of such software for machines ranging from desktop workstations to embedded processors can be a tedious and time-consuming task. ATLAS has been designed to automate much of this process. We concentrate our efforts on the widely used linear algebra kernels called the Basic Linear Algebra Subroutines (BLAS). In particular, our initial work is for general matrix multiply, DGEMM. However much of the technology and approach developed here can be applied to the other Level 3 BLAS. The general strategy can have an impact on basic linear algebra operations in general and may be extended to other important kernel operations, such as sparse operations.
ATLAS uses code generators (i.e., programs that write other programs) in order to provide the many different ways of doing a given operation, and has sophisticated search scripts and robust timing mechanisms in order to find the best ways of performing the operation for a given architecture.
One of the main performance kernels of linear algebra has traditionally been a standard API known as the BLAS (Basic Linear Algebra Subprograms). This API is supported by hand-tuned efforts of many hardware vendors, and thus provides a good first target for ATLAS, as there is both a large audience for this API, and on those platforms where vendor-supplied BLAS exist, an easy way to see if ATLAS can provide the required level of performance.
Results and Interactions:
The ATLAS project just released version 3.0BETA of the package. Highlights of changes from v2.0 are:
Therefore, this is the first release that supplies a complete, highly optimal, BLAS package. Timings (some of which can be found at http://www.netlib.org/atlas) show that ATLAS provides a portable library that competes favorably on a wide variety of architectures with the traditional hand-tuned libraries. As mentioned in the highlights above, we have begun to look at optimizations in other areas as well. There are many areas that require further investigation; we detail a few of them below. We plan to perform preliminary investigations into most if not all of the areas in the next 18 months, and expect to more fully investigate several.
Plans:
Results and Interactions:

We are working with researchers at LLNL to extend these ideas to sparse matrix operations.
PAPI
Overview:
The purpose of the PAPI project is to specify a standard application-programming interface (API) for accessing hardware performance counters available on most modern microprocessors. These counters exist as a small set of registers that count events, which are occurrences of specific signals related to the processor's function. Monitoring these events facilitates correlation between the structure of source/object code and the efficiency of the mapping of that code to the underlying architecture. This correlation has a variety of uses in performance analysis including hand tuning, compiler optimization, debugging, benchmarking, monitoring and performance modeling. In addition, it is hoped that this information will prove useful in the development of new compilation technology as well as in steering architectural development towards alleviating commonly occurring bottlenecks in high performance computing.
Results and Interactions:
This project is just beginning. We expect this effort to have an impact on performance tuning and analysis of users programs.
This project is part of the Parallel Tools Consortium.
Faster Eigensolvers and SVD
Overview:
There are two recent algorithmic innovations made by our groups and other for solving the symmetric eigenvalue problem and singular value decomposition (SVD). In both cases the algorithms have three phases: First, we reduce the initial matrix from dense (or banded or sparse...) to narrow band form (tridiagonal for the symmetric eigenvalue problem, and bidiagonal for the SVD). Second, we solve the eigenproblem or SVD for the narrow band matrix. Third, we transform the solution of the narrow band problem to the original problem. Phases 1 and 3 are basically well-parallelized, and use the BLAS effectively (but see the section on the BLAST Forum for innovations here too). But Phase 2 is the bottleneck if we use the traditional QR algorithm, which leads us to seek better alternatives.The first alternative to QR is based on a divide-and-conquer algorithm (DC) introduced by Cuppen in the early 80s, but not made effective and stable until the early 1990s by the work of Ming Gu and Stan Eisenstat. This drops the O(n3) complexity of QR to O(nx) for some x typically much less than 3, but still 3 in the worst case. Furthermore, it uses the BLAS effectively, whereas QR is BLAS1 only. This was incorporated into LAPACK v 2.0 in 1994 just for the symmetric eigenvalue problem. It is not straightforward to parallelize because of communication.
The second alternative is much more recent, based on work by Prof. Beresford Parlett and Inderjit Dhillon at Berkeley. We call it the Holy Grail (HG) because it enjoys the two properties of (1) requiring only the minimal O(nk) work to compute the nk entries of k different eigenvectors of dimension n, and (2) being able to compute each requested eigenvector in an embarrassingly parallel fashion. The Holy Grail assumes IEEE arithmetic, and exploits NAN and infinity arithmetic to go faster; this is first LAPACK routine that requires IEEE arithmetic to work correctly, and represents a break from the past where we insisted on portability to older architectures like the Cray C90.
This is joint work with several other people as well, including Osni Marques at NERSC.
Results and Interactions:
LAPACK v. 3, released in mid 1999, along with an updated Users' Guide, includes both (1) the Holy Grail (HG) implementation of the dense and tridiagonal symmetric eigenvalue problems, and (2) divide-and-conquer (DC) algorithms for the SVD and SVD-based least squares solver.
The figures in Section 3.5 of the Users' Guide, the LAPACK Benchmark show how much faster the new algorithms are than the old.
We first consider the Holy Grail. The figure below, figure 3.1 from the Users' Guide, compares the performance of three routines, DSTEQR, DSTEDC and DSTEGR, for coputing all the eigenvalues and eigenvectors of a symmetric tridiagonal matrix. The times are shown on a Compaq AlphaServer DS-20 for matrix dimensions from 100 to 1000. DSTEQR (QR) was the only algorithm available in LAPACK 1.0, DSTEDC (divide-and-conquer) was introduced in LAPACK 2.0, and DSTEGR (the Holy Grail) was introduced in LAPACK 3.0. As can be seen, for large matrices DSTEQR is about 14 times faster than DSTEDC and nearly 50 times faster than DSTEQR.
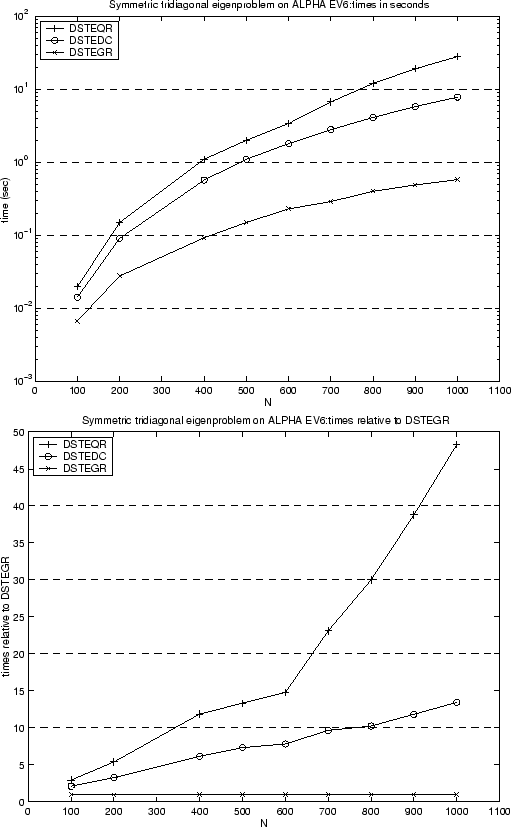
|
We next consider the full singular value decomposition of a dense 1000 by 1000 matrix. We compare DGESVD, the original QR-based routines from LAPACK 1.0, with DGESDD, the new divide-and-conquer based routine from LAPACK 3.0. The table below shows the speeds on several machines. The new routine is 5.7 to 16.8 times faster than the old routine. Part of the speed results from doing many fewer operations, and the rest comes from doing them faster (a high Mflop rate).
---------------------------------------------------------------------------------
| Machine Peak Old routine New routine Speedup of |
| Mflops Time Mflops Time Mflops New vs Old |
| (DGEMM) (secs) (secs) |
| ----------- ------ --------------- --------------- ---------- |
| Compaq AS DS-20 500 143 107 21 323 6.8 |
| IBM Power 3 722 252 61 15 438 16.8 |
| Intel Pentium III 400 245 62 39 171 6.3 |
| SGI Origin 2000 555 176 87 25 267 7.0 |
| SUN Enterprise 450 527 402 38 71 94 5.7 |
---------------------------------------------------------------------------------
Finally consider the figure below (figure 3.3 in the Users' Guide), which compares the performance of five drivers for the linear least squares problem, DGELS, DGELSY, DGELSX, DGELSD and DGELSS, which are shown in order of decreasing speed. DGELS is the fastest, using just QR without pivoting, and so also the least reliable for rank deficient problems. DGELSY and DGELSX use QR with pivoting, and so handle rank-deficient problems more reliably than DGELS, but can be more expensive. DGELSD and DGELSS both use the SVD, and so are the most reliable (and expensive) ways to solve rank deficient least squares problems. DGELS, DGELSX and DGELSS were in LAPACK 1.0, and DGELSY and DGELSD where introduced in LAPACK 3.0. DGELDS uses the new divide and conquer algorithm. The times are shown on a Compaq AlphaServer DS-20 for square matrices of dimensions from 100 to 1000, and for one right-hand-side. Note that DGELSD is only 3 to 5 times slower than the fastest algorithm DGELS, whereas the old algorithm DGELSS that it replaces was 7 to 34 times slower.
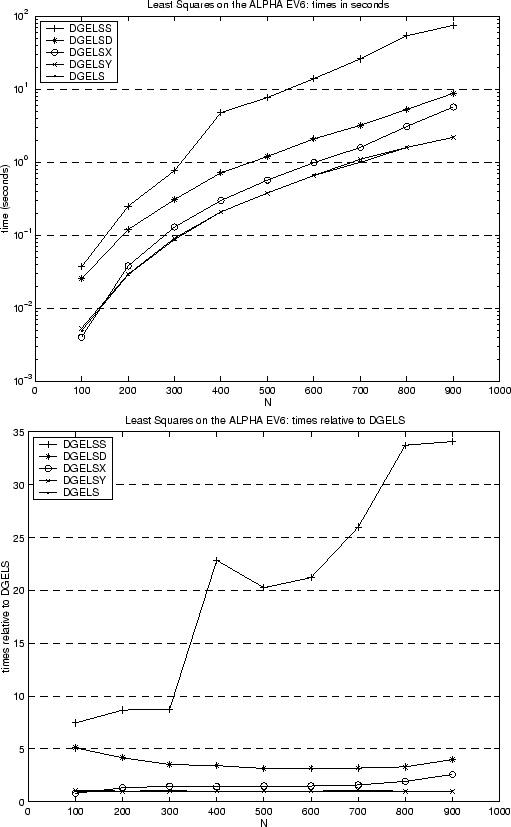
|
Future Plans:
Basic Linear Algebra Subprogram (BLAS) Technical Forum
Overview:
The BLAS Technical Forum is a standards committee with representatives from academia, industry, and national labs. Its mandate is to extend the widely used BLAS to include
Results and Interactions:
In fall of 1999, the final version of the new BLAS standard was finally approved. This 323 page document describes in great detail the calling sequences and semantics of hundreds of new routines, in Fortran 77, Fortran 95 and C. It is available on the BLAS Technical Forum web page.
We are now engaged in providing a reference implementation, including test code. The sparse BLAS (chapter 3) are being implemented by Iain Duff and his collaborations at Rutherford in England. Berkeley is implementing chapter 4 (extended and mixed precision BLAS) using a technique based on M4 macros, that will also implement a large fraction of chapter 2 (dense and banded BLAS, with conventional precisions). Collaborators at HP/Convex are using our M4 templates to implement the rest of Chapter 2.
The work at Berkeley is joint with Xiaoye Li at NERSC and a team of 6 undergraduates. The current Berkeley implementation includes all the real versions of three routines: DOT, SPMV and GBMV, as well as test code. There are many versions of each routine, because of the used of extended and mixed precision (e.g. taking the dot product of one single precision real arrays with one single precision complex array, returning the single precision complex result, and doing intermediate computations in double-double, or about 106 bits of precision). This made the use of M4 to automatically generate code from templates essential. For example, 220 lines of M4 for DOT expand into 9526 lines of C, including all versions.
Testing is the biggest challenge, since we want to portably test semantics like the one mentioned above (single precision inputs and output, extended precision internally) without resorting to extended precision packages in the test code. We have done this by systematically generating test arrays in any precision and of any length whose dot product is extremely small. Comparing the computed dot product with the true dot product exposes the actual internal precision used. Testing other routines (like matrix-vector multiply) can be reduced to testing dot products.
Future Plans:
SuperLU
Overview:
SuperLU is a general purpose library for the direct solution of large, sparse, nonsymmetric systems of linear equations on high performance machines. The library is written in C and is callable from either C or Fortran.
The library routines perform an LU decomposition with partial pivoting and triangular system solves through forward and back substitution. The LU factorization routines can handle non-square matrices but the triangular solves are performed only for square matrices. The matrix columns may be preordered (before factorization) either through library or user supplied routines. This preordering for sparsity is completely separate from the factorization. Working precision iterative refinement subroutines are provided for improved backward stability. Routines are also provided to equilibrate the system, estimate the condition number, calculate the relative backward error, and estimate error bounds for the refined solutions.
SuperLU is joint with with Xiaoye Li at NERSC.
Results and Interactions:
We have completed a release of all three versions:
A talk on SuperLU_DIST was given at the 1999 SIAM Parallel Processing conference, and reported significantly better performance than that in the Supercomputing 98 paper. SuperLU_Dist demonstrated up to 100-fold speedup on the 512 process Cray T3E at NERSC, and up to a 10.2 Gigaflops factorization rate.
SuperLU_DIST was used by C. W. McCurdy and collaborators at LBNL to compute the quantum scattering of a 3-body system, achieving good agreement with experimental data for the first time. The computations involved sparse complex linear systems of dimension up to 1.79 million, which were solved on the SGI/Cray T3E at NERSC and ASCI Blue Pacific Computer at LLNL. This work resulted in the 24 Dec 1999 cover of Science, depicting wavefunctions of the three scattered particles:

Future Plans:
Prometheus
Overview:
Prometheus is a multigrid solver for finite element matrices on unstructured meshes in solid mechanics. Prometheus is joint work with Prof. R. Taylor of Civil Engineering and postdoc Mark Adams. Prometheus is not directly funded by DOE2000, but we include it since it uses PETSc, a DOE2000-supported project.
Prometheus uses maximal independent sets on modified matrix graphs; these node sets are meshed with a Delaunay mesher to provide coarse "grids", which are used with standard finite element shape functions to provide interpolation operators for multigrid. Coarse grid operators are formed with these interpolation operators and the finer grid matrix in a standard Galerkin way. Prometheus is built on PETSc from Argonne National Laboratory, and uses ParMetis from the University of Minnesota and FEAP from the University of California at Berkeley. Its basic architechture is shown below:

Results and Interactions:
Prometheus has solved problems of over 39 million degrees of freedom on 960 PowerPC processors at LLNL with about 60% parallel efficiency. It has solved problems up to 76 million degrees of freedom on 1024 processor This problem was so large that it resulted in paging to disk, so the parallel efficiency decreased, but it did work.
Prometheus is publically available, and being incorporated into applications within ASCI.
Our work on Prometheus was recognized with the
Karl Benz Award for the best industrial application,
in the Mannheim SuParCup '99
at the Mannheim Supercomputer '99 Conference, June 10-12, 1999.
The title of the paper was
"Parallel Unstructured Multigrid Finite Element Solvers."
Future Plans:
PBody
Overview:
Pody is a parallel library of N-body methods, i.e. for quickly calculating the electrostatic or gravitational forces or potentials on N particles. It is portable across a range of parallel machines, permits the user a wide range of choices in how the computation is done, and is efficient.
Pbody was not part of the original DOE2000 proposal, but is work that was going on independently. As Pbody reached maturity, I began supporting the graduate student doing the work, David Blackston.
Results and Interactions:
We have collaborated with Prof. Andy Neureuther at Berkeley to incorporate Pbody into
his EBEAM program for simulating electon beam semiconductor fabrication devices.
A paper "Integration of an adaptive parallel N-body solver into a particle-by-particle
electron beam interation simulation", coauthored by D. Blackston, J. Demmel, A. Neureuther and
B. Wu, was presented at Technical Conference 3777,
Charged Particle Optics IV, part of the annual SPIE meeting,
22-23 July 1999.
Future Plans: