| Brian
Harvey University of California, Berkeley |
| Download PDF version |
| Back to Table of Contents |
| BACK chapter thread NEXT |
| MIT Press web page for Computer Science Logo Style |
|
|
Program file for this chapter: student
Can a computer be intelligent? What would it mean for a computer to be intelligent? John McCarthy, one of the founders of artificial intelligence research, once defined the field as "getting a computer to do things which, when done by people, are said to involve intelligence." The point of the definition was that he felt perfectly comfortable about carrying on his research without first having to defend any particular philosophical view of what the word "intelligence" means.
There have always been two points of view among AI researchers about what their purpose is. One point of view is that AI programs contribute to our understanding of human psychology; when researchers take this view they try to make their programs reflect the actual mechanisms of intelligent human behavior. For example, Allen Newell and Herbert A. Simon begin their classic AI book Human Problem Solving with the sentence, "The aim of this book is to advance our understanding of how humans think." In one of their research projects they studied cryptarithmetic problems, in which digits are replaced with letters in a multi-digit addition or multiplication. First they did a careful observation and analysis of how a human subject attacked such a problem, then they pointed out specific problem-solving techniques that the person used, and used those techniques as the basis for designing a computer simulation. The other point of view is that AI programs provide a more abstract model for intelligence in general; just as one can learn about the properties of computers by studying finite-state machines, even though no real computer operates precisely as a formal finite-state machine does, we can learn about the properties of any possible intelligent being by simulating intelligence in a computer program, whether or not the mechanisms of that program are similar to those used by people.
In the early days of AI research these two points of view were not sharply divided. Sometimes the same person would switch from one to the other, sometimes trying to model human thought processes and sometimes trying to solve a given problem by whatever methods could be made to work. More recently, researchers who hold one or the other point of view consistently have begun to define two separate fields. One is cognitive science, in which computer scientists join with psychologists, linguists, biologists, and others to study human cognitive psychology, using computer programs as a concrete embodiment of theories about the human mind. The other is called expert systems or knowledge engineering, in which programming techniques developed by AI researchers are put to practical use in programs that solve real-world business problems such as the diagnosis and repair of malfunctioning equipment.
In this chapter I'm going to concentrate on one particular area of AI research: teaching a computer to understand English. Besides its inherent interest, this area has the advantage that it doesn't require special equipment, as do some other parts of AI such as machine vision and the control of robot manipulators.
In the 1950s many people were very optimistic about the use of computers to translate from one language to another. IBM undertook a government-sponsored project to translate scientific journals from Russian to English. At first they thought that this translation could be done very straightforwardly, with a Russian-English dictionary and a few little kludges to rearrange the order of words in a sentence to account for differences in the grammatical structure of the two languages. This simple approach was not successful. One problem is that the same word can have different meanings, and even different parts of speech, in different contexts. (According to one famous anecdote, the program translated the Russian equivalent of "The spirit is willing but the flesh is weak" into "The vodka is strong but the meat is rotten.")
A decade later, several AI researchers had the idea that ambiguities in the meanings of words could be resolved by trying to understand English only in some limited context. If you know in advance that the sentence you're trying to understand is about baseball statistics, or about relationships in a family tree, or about telling a robot arm to move blocks on a table (these are actual examples of work done in that period) then only certain narrowly defined types of sentences are meaningful at all. You needn't think about metaphors or about the many assumptions about commonsense knowledge that people make in talking with one another. Such a limited context for a language understanding program is called a microworld.
This chapter includes a Logo version of Student, a program written by Daniel G. Bobrow for his 1964 Ph.D. thesis, Natural Language Input for a Computer Problem Solving System, at MIT. Student is a program that solves algebra word problems:
? student [The price of a radio is 69.70. If this price is 15 percent
less than the marked price, find the marked price.]
The marked price is 82 dollars
(In this illustration I've left out some of Student's display of intermediate results.) The program has two parts: one that translates the word problem into the form of equations and another that solves the equations. The latter part is complex (about 40 Logo procedures) but straightforward; it doesn't seem surprising to most people that a computer can manipulate mathematical equations. It is Student's understanding of English sentences that furthered the cause of artificial intelligence.
The aim of the research reported here was to discover how one could build a computer program which could communicate with people in a natural language within some restricted problem domain. In the course of this investigation, I wrote a set of computer programs, the Student system, which accepts as input a comfortable but restricted subset of English which can be used to express a wide variety of algebra story problems...
In the following discussion, I shall use phrases such as "the computer understands English." In all such cases, the "English" is just the restricted subset of English which is allowable as input for the computer program under discussion. In addition, for purposes of this report I have adopted the following operational definition of understanding. A computer understands a subset of English if it accepts input sentences which are members of this subset, and answers questions based on information contained in the input. The Student system understands English in this sense. [Bobrow, 1964.]
How does the algebra microworld simplify the understanding problem? For one
thing, Student need not know anything about the meanings of noun phrases.
In the sample problem above, the phrase The price of a radio is used
as a variable name. The problem could just as well have been
The weight of a giant size detergent box is 69.70 ounces. If this weight is 15 percent less than the weight of an enormous size box, find the weight of an enormous size box.
For Student, either problem boils down to
variable1 = 69.70 units variable1 = 0.85 * variable2 Find variable2.
Student understands particular words only to the extent that they
have a mathematical meaning. For example, the program knows that
15 percent less than means the same as 0.85 times.
Student translates a word problem into equations in several steps. In the following paragraphs, I'll mention in parentheses the names of the Logo procedures that carry out each step I describe, but don't read the procedures yet. First read through the description of the process without worrying about the programming details of each step. Later you can reread this section while examining the complete listing at the end of the chapter.
In translating Student to Logo, I've tried not to change the capabilities of the program in any way. The overall structure of my version is similar to that of Bobrow's original implementation, but I've changed some details. I've used iteration and mapping tools to make the program easier to read; I've changed some aspects of the fine structure of the program to fit more closely with the usual Logo programming style; in a few cases I've tried to make exceptionally slow parts of the program run faster by finding a more efficient algorithm to achieve the same goal.
The top-level procedure student takes one input, a list containing the
word problem. (The disk file that accompanies this project includes several
variables containing sample problems. For example,
? student :radio
will carry out the steps I'm about to describe.) Student begins by printing the original problem:
? student :radio The problem to be solved is The price of a radio is 69.70. If this price is 15 percent less than the marked price, find the marked price.
The first step is to separate punctuation characters from the
attached words. For example, the word "price," in the original problem
becomes the two words "price ," with the comma on its own. Then
(student1) certain mandatory substitutions are applied
(idioms). For example, the phrase percent less than is translated
into the single word perless. The result is printed:
With mandatory substitutions the problem is The price numof a radio is 69.70 dollars . If this price is 15 perless the marked price , find the marked price .
(The word of in an algebra word problem can have two
different meanings. Sometimes it means "times," as in the phrase
"one half of the population." Other times, as in this problem, "of" is
just part of a noun phrase like "the price of a radio." The special word
numof is a flag to a later part of the program and will then be
further translated either into times or back into of. The
original implementation of Student used, instead of a special word like
numof, a "tagged" word represented as a list like [of / op]. Other
examples of tagging are [Bill / person] and [has / verb].)
The next step is to separate the problem into simple sentences (bracket):
The simple sentences are The price numof a radio is 69.70 dollars . This price is 15 perless the marked price . Find the marked price .
Usually this transformation of the problem is straightforward, but the special case of "age problems" is recognized at this time, and special transformations are applied so that a sentence like
Mary is 24 years old.
is translated into
Mary s age is 24 .
An age problem is one that contains any of the phrases as old
as, age, or years old.
The next step is to translate each simple sentence into an equation or a
variable whose value is desired as part of the solution (senform).
The equations to be solved are Equal [price of radio] [product 69.7 [dollars]] Equal [price of radio] [product 0.85 [marked price]]
The third simple sentence is translated, not into an equation, but
into a request to solve these equations for the variable marked price.
The translation of simple sentences into equations is the most
"intelligent" part of the program; that is, it's where the program's
knowledge of English grammar and vocabulary come into play and many special
cases must be considered. In this example, the second simple sentence
starts with the phrase this price. The program recognizes the word
this (procedure nmtest) and replaces the entire phrase with the
left hand side of the previous equation (procedure this).
Student analyzes a sentence by comparing it to several patterns
(senform1). For example, one sentence form that Student understands
is exemplified by these sentences:
Joe weighs 163 pounds . The United States Army has 8742 officers .
The general pattern is
something verb number unit .
Student treats such sentences as if they were rearranged to match
The number of unit something verb is number .
and so it generates the equations
Equal [number of pounds Joe weighs] 163 Equal [number of officers United States Army has] 8742
The original version of Student was written in a pattern matching language called Meteor, which Bobrow wrote in Lisp. In Meteor, the instruction that handles this sentence type looks like this:
(* ( (1 / verb) (fn nmtest) 1 (1 / dlm)) 0
(/ (*s shelf (*k equal (fn opform (*k the number of 4 1 2))
(fn opform (*k 3 5 6))))) return)
The top line contains the pattern to be matched. In the pattern,
a dollar sign represents zero or more words; the notation 1
represents a single word. The zero at the end of the line means that the
text that matches the pattern should be deleted and nothing should replace
it. The rest of the instruction pushes a new equation onto a stack named
shelf; that equation is formed out of the pieces of the matched
pattern according to the numbers in the instruction. That is, the number
4 represents the fourth component of the pattern, which is 1.
Here is the corresponding instruction in the Logo version:
if match [^one !verb1:verb !factor:numberp #stuff1 !:dlm] :sent
[output (list (list "equal
opform (sentence [the number of]
:stuff1 :one :verb1)
opform (list :factor) ))]
The pattern matcher I used for Student is the same as the one in Advanced Techniques, the second volume of this series.* Student often relies on the fact that Meteor's pattern matcher finds the first substring of the text that matches the pattern, rather than requiring the entire text to match. Many patterns in the Logo version therefore take the form
[^beg interesting part #end]
where the "interesting part" is all that appeared in the Meteor pattern.
*The
version in this project is modified slightly; the
match procedure
first does a fast test to try to reject an irrelevant pattern in O(n)
time before calling the actual pattern matcher, which could take as much
as O(2n) time to reject a pattern, and which has been renamed rmatch
(for "real match") in this project.
Here is a very brief summary of the Logo pattern matcher included in this
program. For a fuller description with examples, please refer to Volume 2.
Match is a predicate with two inputs, both lists. The first input is
the pattern and the second input is the sentence. Match
outputs true if the sentence matches the pattern. A word in
the pattern that does not begin with one of the special quantifier
characters listed below matches the identical word in the sentence. A word
in the pattern that does begin with a quantifier matches zero or more words
in the sentence, as follows:
# | zero or more |
& | one or more |
? | zero or one |
! | exactly one |
@ | zero or more (test as group) |
^ | zero or more (as few as possible) |
All quantifiers match as many consecutive words as possible while
still allowing the remaining portion of the pattern to be matched, except
for ^. A quantifier may be used alone, or it can be followed by a
variable name, a predicate name, or both:
# #var #:pred #var:predIf a variable name is used, the word or words that match the quantifier will be stored in that variable if the match is successful. (The value of the variable if the match is not successful is not guaranteed.) If a predicate is used, it must take one word as input; in order for a word in the sentence to be accepted as (part of) a match for the quantifier, the predicate must output
true when given that word as input. For
example, the word
!factor:numberp
in the pattern above requires exactly one matching word in the
sentence; that word must be a number, and it is remembered in the variable
factor. If the quantifier is @ then the predicate must take a
list as input, and it must output true for all the candidate
matching words taken together as a list. For example, if you define a
procedure
to threep :list output equalp count :list 3 end
then the pattern word
@:threep
will match exactly three words in the sentence. (Student does not
use this last feature of the pattern matcher. In fact, predicates are
applied only to the single-word quantifiers ? and !.)
Pattern matching is also heavily used in converting words and phrases with
mathematical meaning into the corresponding arithmetic operations
(opform). An equation is a list of three members; the first member is the
word equal and the other two are expressions formed by applying
operations to variables and numbers. Each operation that is required is
represented as a list whose first member is the name of the Logo procedure
that carries out the operation and whose remaining members are expressions
representing the operands. For example, the equation
would be represented by the list
[equal [y] [sum [product 3 [square [x]]] [product 6 [x]] [minus 1]]]
The variables are represented by lists like [x] rather than
just the words because in Student a variable can be a multi-word phrase like
price of radio. The difference between two expressions is represented
by a sum of one expression and minus the other, rather than as
the difference of the expressions, because this representation turns
out to make the process of simplifying and solving the equations easier.
In word problems, as in arithmetic expressions, there is a precedence of
operations. Operations like squared apply to the variables right next
to them; ones like times are intermediate, and ones like plus
apply to the largest possible subexpressions. Student looks first for the
lowest-priority ones like plus; if one is found, the entire rest of
the clause before and after the operation word provide the operands. Those
operands are recursively processed by opform; when all the
low-priority operations have been found, the next level of priority will be
found by matching the pattern
[^left !op:op1 #right]
Student uses the substitution technique to solve the equations. That is, one equation is rearranged so that the left hand side contains only a single variable and the right hand side does not contain that variable. Then, in some other equation, every instance of that variable is replaced by the right hand side of the first equation. The result is a new equation from which one variable has been eliminated. Repeating this process enough times should eventually yield an equation with only a single variable, which can be solved to find the value of that variable.
When a problem gives rise to several linear equations in several variables, the traditional technique for computer solution is to use matrix inversion; this technique is messy for human beings because there is a lot of arithmetic involved, but straightforward for computers because the algorithm can be specified in a simple way that doesn't depend on the particular equations in each problem. Bobrow chose to use the substitution method because some problems give rise to equations that are linear in the variable for which a solution is desired but nonlinear in other variables. Consider this problem:
? student :tom
The problem to be solved is
If the number of customers Tom gets is twice the square of 20 per cent of
the number of advertisements he runs, and the number of advertisements he
runs is 45, what is the number of customers Tom gets?
With mandatory substitutions the problem is
If the number numof customers Tom gets is 2 times the square 20 percent
numof the number numof advertisements he runs , and the number numof
advertisements he runs is 45 , what is the number numof customers
Tom gets ?
The simple sentences are
The number numof customers Tom gets is 2 times the square 20 percent
numof the number numof advertisements he runs .
The number numof advertisements he runs is 45 .
What is the number numof customers Tom gets ?
The equations to be solved are
Equal [number of customers Tom gets]
[product 2 [square [product 0.2 [number of advertisements
he runs]]]]
Equal [number of advertisements he runs] 45
The number of customers Tom gets is 162
The problem is solved.
The first equation that Student generates for this problem is linear in the number of customers Tom gets, but nonlinear in the number of advertisements he runs. (That is, the equation refers to the square of the latter variable. An equation is linear in a given variable if that variable isn't multiplied by anything other than a constant number.) Using the substitution method, Student can solve the problem by substituting the value 45, found in the second equation, for the number of advertisements variable in the first equation.
(Notice, in passing, that one of the special numof words in this
problem was translated into a multiplication rather than back into the
original word of.)
The actual sequence of steps required to solve a set of equations is quite
intricate. I recommend taking that part of Student on faith the first time
you read the program, concentrating instead on the pattern matching
techniques used to translate the English sentences into equations. But here
is a rough guide to the solution process. Both student1 and
student2 call trysolve with four inputs: a list of the equations to
solve, a list of the variables for which values are wanted, and two lists of
units. A unit is a word or phrase like dollars or feet
that may be part of a solution. Student treats units like variables while
constructing the equations, so the combination of a number and a unit is
represented as a product, like
[product 69.7 [dollars]]
for 69.70 in the first sample problem. While constructing the
equations, Student generates two lists of units. The first, stored in the
variable units, contains any word or phrase that appears along with a
number in the problem statement, like the word feet in the phrase
3 feet (nmtest). The second, in the variable aunits, contains
units mentioned explicitly in the find or how many sentences
that tell Student what variables should be part of the solution
(senform1). If the problem includes a sentence like
How many inches is a yard?
then the variable [inches], and only that variable,
is allowed to be part of the answer. If there are no aunits-type
variables in the problem, then any of the units variables may appear
in the solution (trysolve).
Trysolve first calls solve to solve the equations and then uses
pranswers to print the results. Solve calls solver to do
most of the work and then passes its output through solve.reduce for
some final cleaning up. Solver works by picking one of the
variables from the list :wanted and asking solve1 to find a
solution for that variable in terms of all the other variables--the
other wanted variables as well as the units allowed in the ultimate answer.
If solve1 succeeds, then solver invokes itself,
adding the newly-found expression for one variable to an
association list (in the variable alis) so that, from then
on, any occurrence of that variable will be replaced with the equivalent
expression. In effect, the problem is simplified by eliminating one
variable and eliminating one equation, the one that was solved to find the
equivalent expression.
Solve1 first looks for an equation containing the variable for which
it is trying to find a solution. When it finds such an equation, the next
task is to eliminate from that equation any variables that aren't part of
the wanted-plus-units list that solver gave solve1 as an input.
To eliminate these extra variables, solve1 invokes solver with
the extras as the list of wanted variables. This mutual recursion between
solver and solve1 makes the structure of the solution process
difficult to follow. If solver manages to eliminate the extra
variables by expressing them in terms of the originally wanted ones, then
solve1 can go on to substitute those expressions into its originally
chosen equation and then use solveq to solve that one equation for the
one selected variable in terms of all the other allowed variables.
Solveq manipulates the equation more or less the way students in algebra
classes do, adding the same term to both sides, multiplying both sides by
the denominator of a polynomial fraction, and so on.
Here is how solve solves the radio problem. The equations, again, are
Equal [price of radio] [product 69.7 [dollars]] Equal [price of radio] [product 0.85 [marked price]]
Trysolve evaluates the expression
(1) solve [[marked price]]
[[equal [price of radio] [product 69.7 [dollars]]]
[equal [price of radio] [product 0.85 [marked price]]] ]
[[dollars]]
(I'm numbering these expressions so that I can refer to them later
in the text.) The first input to solve is the list of variables
wanted in the solution; in this case there is only one such variable. The
second input is the list of two equations. The third is the list of unit
variables that are allowed to appear in the solution; in this case only
[dollars] is allowed. Solve evaluates
(2) solver [[marked price]] [[dollars]] [] []
(There is a fifth input, the word insufficient, but this is
used only as an error flag if the problem can't be solved. To simplify this
discussion I'm going to ignore that input for both solver and
solve1.) Solver picks the first (in this case, the only) wanted
variable as the major input to solve1:
(3) solve1 [marked price]
[[dollars]]
[]
[[equal [price of radio] [product 69.7 [dollars]]]
[equal [price of radio] [product 0.85 [marked price]]] ]
[]
Notice that the first input to solve1 is a single variable,
not a list of variables. Solve1 examines the first equation in the
list of equations making up its fourth input. The desired variable does not
appear in this equation, so solve1 rejects that equation and invokes
itself recursively:
(4) solve1 [marked price]
[[dollars]]
[]
[[equal [price of radio] [product 0.85 [marked price]]]]
[[equal [price of radio] [product 69.7 [dollars]]]]
This time, the first (and now only) equation on the list of
candidates does contain the desired variable. Solve1 removes that
equation, not from its own list of equations (:eqns), but from
solve's overall list (:eqt). The equation, unfortunately, can't be
solved directly to express [marked price] in terms of [dollars],
because it contains the extra, unwanted variable [price of radio].
We must eliminate this variable by solving the remaining equations for it:
(5) solver [[price of radio]] [[marked price] [dollars]] [] []
As before, solver picks the first (again, in this case, the
only) wanted variable and asks solve1 to solve it:
(6) solve1 [price of radio]
[[marked price] [dollars]]
[]
[[equal [price of radio] [product 69.7 [dollars]]]]
[]
Solve1 does find the desired variable in the first (and
only) equation, and this time there are no extra variables. Solve1
can therefore ask solveq to solve the equation:
(7) solveq [price of radio]
[equal [price of radio] [product 69.7 [dollars]]]
It isn't part of solveq's job to worry about which variables
may or may not be part of the solution; solve1 doesn't call
solveq until it's satisfied that the equation is okay.
In this case, solveq has little work to do because the equation is
already in the desired form, with the chosen variable alone on the left side
and an expression not containing that variable on the right.
solveq (7) outputs [[price of radio] [product 69.7 [dollars]]
to solve1 (6)
Solve1 appends this result to the previously empty
association list.
solve1 (6) outputs [[[price of radio] [product 69.7 [dollars]]]
to solver (5)
Solver only had one variable in its :wanted list, so
its job is also finished.
solver (5) outputs [[[price of radio] [product 69.7 [dollars]]]
to solve1 (4,3)
This outer invocation of solve1 was trying to solve for
[marked price] an equation that also involved [price of radio].
It is now able to use the new association list to substitute for this
unwanted variable an expression in terms of wanted variables only; this
modified equation is then passed on to solveq:
(8) solveq [marked price]
[equal [product 69.7 [dollars]] [product 0.85 [marked price]]]
This time solveq has to work a little harder, exchanging the
two sides of the equation and dividing by 0.85.
solveq (8) outputs [[marked price] [product 82 [dollars]]]
to solve1 (4,3)
Solve1 appends this result to the association list:
solve1 (4,3) outputs [[[price of radio] [product 69.7 [dollars]]]
[[marked price] [product 82 [dollars]]] ]
to solver (2)
Since solver has no other wanted variables, it outputs the
same list to solve, and solve outputs the same list to
trysolve. (In this example, solve.reduce has no effect because all
of the expressions in the association list are in terms of allowed units
only. If the equations had been different, the expression for [price
of radio] might have included [marked price] and then
solve.reduce would have had to substitute and simplify (subord).)
It'll probably take tracing a few more examples and beating your head
against the wall a bit before you really understand the structure of
solve and its subprocedures. Again, don't get distracted by this part of
the program until you've come to understand the language processing part,
which is our main interest in this chapter.
The main reason why Student treats age problems specially is that the
English form of such problems is often expressed as if the variables were
people, like "Bill," whereas the real variable is "Bill's age." The
pattern matching transformations look for proper names (personp) and
insert the words s age after them (ageify). The first such age
variable in the problem is remembered specially so that it can be
substituted for pronouns (agepron). A special case is the phrase
their ages, which is replaced (ageprob) with a list of all the age
variables in the problem.
? student :uncle
The problem to be solved is
Bill's father's uncle is twice as old as Bill's father. 2 years from now
Bill's father will be 3 times as old as Bill. The sum of their ages is
92 . Find Bill's age.
With mandatory substitutions the problem is
Bill s father s uncle is 2 times as old as Bill s father . 2 years
from now Bill s father will be 3 times as old as Bill . sum their
ages is 92 . Find Bill s age .
The simple sentences are
Bill s father s uncle s age is 2 times Bill s father s age .
Bill s father s age pluss 2 is 3 times Bill s age pluss 2 .
Sum Bill s age and Bill s father s age and Bill s father s uncle s age
is 92 .
Find Bill s age .
The equations to be solved are
Equal [Bill s father s uncle s age] [product 2 [Bill s father s age]]
Equal [sum [Bill s father s age] 2] [product 3 [sum [Bill s age] 2]]
Equal [sum [Bill s age]
[sum [Bill s father s age] [Bill s father s uncle s age]]] 92
Bill s age is 8
The problem is solved.
(Note that in the original problem statement there is a space
between the number 92 and the following period. I had to enter the
problem in that form because of an inflexibility in Logo's input parser,
which assumes that a period right after a number is part of the number, so
that "92." is reformatted into 92 without the dot.)
Student represents the possessive word Bill's as the two words
Bill s because this representation allows the pattern matcher to
manipulate the possessive marker as a separate element to be matched.
A phrase like as old as is just deleted (ageprob) because the
transformation from people to ages makes it redundant.
The phrase 2 years from now in the original problem is first
translated to in 2 years. This phrase is further processed according
to where it appears in a sentence. When it is attached to a particular
variable, in a phrase like Bill s age in 2 years, the entire phrase is
translated into the arithmetic operation Bill s age pluss 2 years
(agewhen). (The special word pluss is an addition operator,
just like plus, except for its precedence; opform treats it as a
tightly binding operation like squared instead of a loosely binding
one like the ordinary plus.) When a phrase like in 2 years
appears at the beginning of a sentence, it is remembered (agesen) as
an implicit modifier for every age variable in that sentence that
isn't explicitly modified. In this example, in 2 years modifies both
Bill s father s age and Bill s age. The special precedence of
pluss is needed in this example so that the equation will be based on
the grouping
3 times [ Bill s age pluss 2 ]
rather than
[ 3 times Bill s age ] plus 2
as it would be with the ordinary plus operator. You can
also see how the substitution for their ages works in this example.
Here is a second sample age problem that illustrates a different kind of special handling:
? student :ann The problem to be solved is Mary is twice as old as Ann was when Mary was as old as Ann is now. If Mary is 24 years old, how old is Ann? With mandatory substitutions the problem is Mary is 2 times as old as Ann was when Mary was as old as Ann is now . If Mary is 24 years old , what is Ann ? The simple sentences are Mary s age is 2 times Ann s age minuss g1 . Mary s age minuss g1 is Ann s age . Mary s age is 24 . What is Ann s age ? The equations to be solved are Equal [Mary s age] [product 2 [sum [Ann s age] [minus [g1]]]] Equal [sum [Mary s age] [minus [g1]]] [Ann s age] Equal [Mary s age] 24 Ann s age is 18 The problem is solved.
What is new in this example is Student's handling of the phrase was
when in the sentence
Mary is 2 times as old as Ann was when Mary was as old as Ann is now .
Sentences like this one often cause trouble for human algebra students
because they make implicit reference to a quantity that is not
explicitly present as a variable. The sentence says that Mary's age
now is twice Ann's age some number of years ago, but that number
is not explicit in the problem. Student makes this variable explicit by
using a generated symbol like the word g1 in this illustration.
Student replaces the phrase was when with the words
was g1 years ago . g1 years ago
This substitution (in ageprob) happens before the
division of the problem statement into simple sentences (bracket). As
a result, this one sentence in the original problem becomes the two sentences
Mary s age is 2 times Ann s age g1 years ago . G1 years ago Mary s age was Ann s age now .
The phrase g1 years ago in each of these sentences is
further processed by agesen and agewhen as discussed earlier;
the final result is
Mary s age is 2 times Ann s age minuss g1 . Mary s age minuss g1 is Ann s age .
A new generated symbol is created each time this situation arises,
so there is no conflict from trying to use the same variable name for two
different purposes. The phrase will be when is handled similarly,
except that the translated version is
in g2 years . in g2 years
These decoupling heuristics are useful not only for the Student program but for people trying to solve age problems. The classic age problem about Mary and Ann, given above, took an MIT graduate student over 5 minutes to solve because he did not know this heuristic. With the heuristic he was able to set up the appropriate equations much more rapidly. As a crude measure of Student's relative speed, note that Student took less than one minute to solve this problem.
This excerpt from Bobrow's thesis illustrates the idea that insights from artificial intelligence research can make a valuable contribution to the education of human beings. An intellectual problem is solved, at least in many cases, by dividing it into pieces and developing a technique for each subproblem. The subproblems are the same whether it is a computer or a person trying to solve the problem. If a certain technique proves valuable for the computer, it may be helpful for a human problem solver to be aware of the computer's methods. Bobrow's suggestion to teach people one specific heuristic for algebra word problems is a relatively modest example of this general theme. (A heuristic is a rule that gives the right answer most of the time, as opposed to an algorithm, a rule that always works.) Some researchers in cognitive science and education have proposed the idea of intelligent CAI (computer assisted instruction), in which a computer would be programmed as a "tutor" that would observe the efforts of a student in solving a problem. The tutor would know about some of the mistaken ideas people can have about a particular class of problem and would notice a student falling into one of those traps. It could then offer advice tailored to the needs of that individual student.
The development of the Logo programming language (and so also, indirectly, this series of books) is another example of the relationship between AI and education. Part of the idea behind Logo is that the process of programming a computer resembles, in some ways, the process of teaching a person to do something. (This can include teaching oneself.) For example, when a computer program doesn't work, the experienced programmer doesn't give up in despair, but instead debugs the program. Yet many students are willing to give up and say "I just don't get it" if their understanding of some problem isn't perfect on the first try.
The critic is afraid that children will adopt the computer as model and eventually come to "think mechanically" themselves. Following the opposite tack, I have invented ways to take educational advantage of the opportunities to master the art of deliberately thinking like a computer, according, for example, to the stereotype of a computer program that proceeds in a step-by-step, literal, mechanical fashion. There are situations where this style of thinking is appropriate and useful. Some children's difficulties in learning formal subjects such as grammar or mathematics derive from their inability to see the point of such a style.
A second educational advantage is indirect but ultimately more important. By deliberately learning to imitate mechanical thinking, the learner becomes able to articulate what mechanical thinking is and what it is not. The exercise can lead to greater confidence about the ability to choose a cognitive style that suits the problem. Analysis of "mechanical thinking" and how it is different from other kinds and practice with problem analysis can result in a new degree of intellectual sophistication. By providing a very concrete, down-to-earth model of a particular style of thinking, work with the computer can make it easier to understand that there is such a thing as a "style of thinking." And giving children the opportunity to choose one style or another provides an opportunity to develop the skill necessary to choose between styles. Thus instead of inducing mechanical thinking, contact with computers could turn out to be the best conceivable antidote to it. And for me what is most important in this is that through these experiences these children would be serving their apprenticeships as epistemologists, that is to say learning to think articulately about thinking. [Seymour Papert, Mindstorms, Basic Books, 1980, p. 27.]
In age problems, as we've just seen, a single sentence may give rise to two equations. Here is an example of the opposite, several sentences that together contribute a single equation.
? student :nums The problem to be solved is A number is multiplied by 6 . This product is increased by 44 . This result is 68 . Find the number. With mandatory substitutions the problem is A number ismulby 6 . This product is increased by 44 . This result is 68 . Find the number . The simple sentences are A number ismulby 6 . This product is increased by 44 . This result is 68 . Find the number . The equations to be solved are Equal [sum [product [number] 6] 44] 68 The number is 4 The problem is solved.
Student recognizes problems like this by recognizing the phrases "is
multiplied by," "is divided by," and "is increased by" (senform1).
A sentence containing one of these phrases is not translated into an
equation; instead, a partial equation is saved until the next
sentence is read. That next sentence is expected to start with a phrase
like "this result" or "this product." The same procedure (this)
that in other situations uses the left hand side of the last equation as the
expression for the this-phrase notices that there is a remembered
partial equation and uses that instead. In this example, the sentence
A number ismulby 6 .
remembers the algebraic expression
[product [number] 6]
The second sentence uses that remembered expression as part of a new, larger expression to be remembered:
[sum [product [number] 6] 44]
The third sentence does not contain one of the special "is increased by" phrases, but is instead a standard "A is B" sentence. That sentence, therefore, does give rise to an equation, as shown above.
Perhaps the most interesting thing to notice about this category of word problem is how narrowly defined Student's criterion for recognizing the category is. Student gets away with it because algebra word problems are highly stereotyped; there are just a few categories, with traditional, standard wordings. In principle there could be a word problem starting
Robert has a certain number of jelly beans. This number is twice the number of jelly beans Linda has.
These two sentences are together equivalent to
The number of jelly beans Robert has is twice the number of jelly beans Linda has.
But Student would not recognize the situation because the first sentence doesn't talk about "is increased by." We could teach Student to understand a word problem in this form by adding the instruction
if match [^one !verb1:verb a certain number of #stuff1 !:dlm] :sent
[push "ref opform (se [the number of] :stuff1 :one :verb1)
op []]
along with the other known sentence forms in senform1.
(Compare this to the pattern matching instruction shown earlier for a
similar sentence but with an explicitly specified number.)
Taking advantage of the stereotyped nature of word problems is an example of how the microworld strategy helped make the early AI programs possible. If word problems were expressed with all the flexibility of language in general, Student would need many more sentence patterns than it actually has. (How many different ways can you think of to express the same idea about Robert and Linda? How many of those ways can Student handle?)
In the examples we've seen so far, Student has relied on the repetition of
identical or near-identical phrases such as "the marked price" or "the
number of advertisements he runs." (The requirement is not quite strictly
identical phrases because articles are removed from the noun phrases to make
variable names.) In real writing, though, such phrases are often
abbreviated when they appear for a second time. Student will translate such
a problem into a system of equations that can't be solved, because what
should be one variable is instead a different variable in each equation.
But Student can recognize this situation and apply heuristic rules to guess
that two similar variable names are meant, in fact, to represent the same
variable. (Some early writers on AI considered the use of heuristic methods
one of the defining characteristics of the field. Computer scientists
outside of AI were more likely to insist on fully reliable algorithms. This
distinction still has some truth to it, but it isn't emphasized so much as a
critical issue these days.) Student doesn't try to equate different
variables until it has first tried to solve the equations as they are
originally generated. If the first attempt at solution fails, Student has
recourse to less certain techniques (student2 calls vartest).
? student :sally
The problem to be solved is
The sum of Sally's share of some money and Frank's share is 4.50.
Sally's share is twice Frank's. Find Frank's and Sally's share.
With mandatory substitutions the problem is
sum Sally s share numof some money and Frank s share is 4.50 dollars .
Sally s share is 2 times Frank s . Find Frank s and Sally s share .
The simple sentences are
Sum Sally s share numof some money and Frank s share is 4.50 dollars .
Sally s share is 2 times Frank s .
Find Frank s and Sally s share .
The equations to be solved are
Equal [sum [Sally s share of some money] [Frank s share]]
[product 4.50 [dollars]]
Equal [Sally s share] [product 2 [Frank s]]
The equations were insufficient to find a solution.
Assuming that
[Frank s] is equal to [Frank s share]
Assuming that
[Sally s share] is equal to [Sally s share of some money]
Frank s is 1.5 dollars
Sally s share is 3 dollars
The problem is solved.
In this problem Student has found two pairs of similar variable names. When it finds such a pair, Student adds an equation of the form
[equal variable1 variable2]
to the previous set of equations. In both of the pairs in this example, the variable that appears later in the problem statement is entirely contained within the one that appears earlier.
Another point of interest in this example is that the variable [dollars]
is included in the list of units that may be part of the answer. The word
problem does not explicitly ask "How many dollars is Sally's share," but
because one of the sentences sets an expression equal to "4.50 dollars"
Student takes that as implicit permission to express the answer in dollars.
The only other condition under which Student will consider two variables
equal is if their names are identical except that some phrase in the one
that appears earlier is replaced with a pronoun in the one that appears
later. That is, a variable like [the number of ice cream cones the
children eat] will be considered equal to a later variable [the number
of ice cream cones they eat]. Here is a problem in which this rule is
applied:
? student :guns
The problem to be solved is
The number of soldiers the Russians have is one half of the number of
guns they have. They have 7000 guns. How many soldiers do they have?
With mandatory substitutions the problem is
The number numof soldiers the Russians have is 0.5 numof the number numof
guns they have . They have 7000 guns . howm soldiers do they have ?
The simple sentences are
The number numof soldiers the Russians have is 0.5 numof the number numof
guns they have .
They have 7000 guns .
Howm soldiers do they have ?
The equations to be solved are
Equal [number of soldiers Russians have]
[product 0.5 [number of guns they have]]
Equal [number of guns they have] 7000
The equations were insufficient to find a solution.
Assuming that
[number of soldiers they have] is equal to
[number of soldiers Russians have]
The number of soldiers they have is 3500
The problem is solved.
In some word problems, not all of the necessary information is contained
within the problem statement itself. The problem requires the student to
supply some piece of general knowledge about the world in order to determine
the appropriate equations. This knowledge may be about unit conversions
(one foot is 12 inches) or about relationships among physical quantities
(distance equals speed times time). Student "knows" some of this
background information and can apply it (geteqns) if the equations
determined by the problem statement are insufficient.
? student :jet
The problem to be solved is
The distance from New York to Los Angeles is 3000 miles. If the average
speed of a jet plane is 600 miles per hour, find the time it takes to
travel from New York to Los Angeles by jet.
With mandatory substitutions the problem is
The distance from New York to Los Angeles is 3000 miles . If the average
speed numof a jet plane is 600 miles per hour , find the time it takes to
travel from New York to Los Angeles by jet .
The simple sentences are
The distance from New York to Los Angeles is 3000 miles .
The average speed numof a jet plane is 600 miles per hour .
Find the time it takes to travel from New York to Los Angeles by jet .
The equations to be solved are
Equal [distance from New York to Los Angeles] [product 3000 [miles]]
Equal [average speed of jet plane]
[quotient [product 600 [miles]] [product 1 [hours]]]
The equations were insufficient to find a solution.
Using the following known relationships
Equal [distance] [product [speed] [time]]
Equal [distance] [product [gas consumption]
[number of gallons of gas used]]
Assuming that
[speed] is equal to [average speed of jet plane]
Assuming that
[time] is equal to [time it takes to travel
from New York to Los Angeles by jet]
Assuming that
[distance] is equal to [distance from New York to Los Angeles]
The time it takes to travel from New York
to Los Angeles by jet is 5 hours
The problem is solved.
Student's library of known relationships is indexed according to the first
word of the name of each variable involved in the relationship. (If a
variable starts with the words number of it is indexed under the
following word.) The relationships, in the form of equations, are stored in
the property lists of these index words.
Property lists are also used to keep track of irregular plurals and the
corresponding singulars. Student tries to keep all units in plural form
internally, so that if a problem refers to both 1 foot and
2 feet the same variable name will be used for both. (That is, the first
of these will be translated into
[product 1 [feet]]
in Student's internal representation. Then the opposite
translation is needed if the product of 1 and some unit appears in an
answer to be printed.
The original Student also used property lists to remember the parts of speech of words and the precedence of operators, but because of differences in the syntax of the Meteor pattern matcher and my Logo pattern matcher I've found it easier to use predicate operations for that purpose.
The original Student system included a separately invoked remember
procedure that allowed all these kinds of global information to be entered
in the form of English sentences. You'd say
Feet is the plural of foot
or
Distance equals speed times time
and remember would use patterns much like those used in
understanding word problems to translate these sentences into pprop
instructions. Since Lisp programs, like Logo programs, can themselves be
manipulated as lists, remember could even accept information of a
kind that's stored in
the Student program itself, such as the wording transformations in
idioms, and modify the program to reflect this information. I haven't
bothered to implement that part of the Student system because it takes up
extra memory and doesn't exhibit any new techniques.
As the above example shows, it's important that Student's search for
relevant known relationships comes before the attempt to equate variables
with similar names. The general relationship that uses a variable named
simply [distance] doesn't help unless Student can identify it as
relevant to the variable named [distance from New York to Los Angeles]
in the specific problem under consideration.
Here is another example in which known relationships are used:
? student :span The problem to be solved is If 1 span is 9 inches, and 1 fathom is 6 feet, how many spans is 1 fathom? With mandatory substitutions the problem is If 1 span is 9 inches , and 1 fathom is 6 feet , howm spans is 1 fathom ? The simple sentences are 1 span is 9 inches . 1 fathom is 6 feet . Howm spans is 1 fathom ? The equations to be solved are Equal [product 1 [spans]] [product 9 [inches]] Equal [product 1 [fathoms]] [product 6 [feet]] Equal g2 [product 1 [fathoms]] The equations were insufficient to find a solution. Using the following known relationships Equal [product 1 [yards]] [product 3 [feet]] Equal [product 1 [feet]] [product 12 [inches]] 1 fathom is 8 spans The problem is solved.
Besides the use of known relationships, this example illustrates two other features of Student. One is the use of an explicitly requested unit in the answer. Since the problem asks
How many spans is 1 fathom?
Student knows that the answer must be expressed in spans.
Had there been no explicit request for a particular unit, all the units that
appear in phrases along with a number would be eligible to appear in the
answer: inches, feet, and fathoms. Student might then
blithely inform us that
1 fathom is 1 fathom The problem is solved.
The other new feature demonstrated by this example is the use of a generated
symbol to represent the desired answer. In the statement of this problem,
there is no explicit variable representing the unknown. [Fathoms] is
a unit, not a variable for which a value could be found. The problem
asks for the value of the expression
[product 1 [fathoms]]
in terms of spans. Student generates a variable name (g2)
to represent the unknown and produces an equation
[equal g2 [product 1 [fathoms]]
to add to the list of equations. A generated symbol will be needed whenever the "Find" or "What is" sentence asks for an expression rather than a simple variable name. For example, an age problem that asks "What is the sum of their ages" would require the use of a generated symbol. (The original Student always used a generated symbol for the unknowns, even if there was already a single variable in the problem representing an unknown. It therefore had equations like
[equal g3 [marked price]]
in its list, declaring one variable equal to another. I chose to check for this case and avoid the use of a generated symbol because the time spent in the actual solution of the equations increases quadratically with the number of equations.)
We have seen many cases in which Student replaces a phrase in the statement
of a problem with a different word or phrase that fits better with the later
stages of processing, like the substitution of 2 times for twice
or a special keyword like perless for percent less than.
Student also has a few cases of optional substitutions that may or
may not be made (tryidiom).
There are two ways in which optional substitutions can happen. One is
exemplified by the phrase the perimeter of the rectangle. Student
first attempts the problem without any special processing of this phrase.
If a solution is not found, Student then replaces the phrase with twice
the sum of the length and width of the rectangle and processes the
resulting new problem from the beginning. Unlike the use of known
relationships or similarity of variable names, which Student handles by
adding to the already-determined equations, this optional substitution
requires the entire translation process to begin again. For example, the
word twice that begins the replacement phrase will be further
translated to 2 times.
The second category of optional substitution is triggered by the phrase
two numbers. This phrase must always be translated to something, because
it indicates that two different variables are needed. But the precise
translation depends on the wording of the rest of the problem. Student
tries two alternative translations: one of the numbers and the other
number and one number and the other number. Here is an example in
which the necessary translation is the one Student tries second:
? student :sumtwo The problem to be solved is The sum of two numbers is 96, and one number is 16 larger than the other number. Find the two numbers. The problem with an idiomatic substitution is The sum of one of the numbers and the other number is 96 , and one number is16 larger than the other number . Find the one of the numbers and the other number . With mandatory substitutions the problem is sum one numof the numbers and the other number is 96 , and one number is 16 plus the other number . Find the one numof the numbers and the other number . The simple sentences are Sum one numof the numbers and the other number is 96 . One number is 16 plus the other number . Find the one numof the numbers and the other number . The equations to be solved are Equal [sum [one of numbers] [other number]] 96 Equal [one number] [sum 16 [other number]] The equations were insufficient to find a solution. The problem with an idiomatic substitution is The sum of one number and the other number is 96 , and one number is 16 larger than the other number . Find the one number and the other number . With mandatory substitutions the problem is sum one number and the other number is 96 , and one number is 16 plus the other number . Find the one number and the other number . The simple sentences are Sum one number and the other number is 96 . One number is 16 plus the other number . Find the one number and the other number . The equations to be solved are Equal [sum [one number] [other number]] 96 Equal [one number] [sum 16 [other number]] The one number is 56 The other number is 40 The problem is solved.
There is no essential reason why Student uses one mechanism rather than another to deal with a particular problematic situation. The difficulties about perimeters and about the phrase "two numbers" might have been solved using mechanisms other than this optional substitution one. For example, the equation
[equal [perimeter] [product 2 [sum [length] [width]]]]
might have been added to the library of known relationships. The difficulty about alternate phrasings for "two numbers" could be solved by adding
[[one of the !word:pluralp] ["one singular :word]]
to the list of idiomatic substitutions in idiom.
Not all the mechanisms are equivalent, however. The "two numbers" problem
couldn't be solved by adding equations to the library of known relationships,
because that phrase appears as part of a larger phrase like "the sum of two
numbers," and Student's understanding of the word sum doesn't allow
it to be part of a variable name. The word sum only makes sense to
Student in the context of a phrase like the sum of . (See procedure
something and something elsetst.sum.)
Sometimes Student fails to solve a problem because the problem is beyond
either its linguistic capability or its algebraic capability. For example,
Student doesn't know how to solve quadratic equations. But sometimes a
problem that Student could solve in principle stumps it because it happens
to lack a particular piece of common knowledge. When a situation like that
arises, Student is capable of asking the user for help (student2).
? student :ship The problem to be solved is The gross weight of a ship is 20000 tons. If its net weight is 15000 tons, what is the weight of the ships cargo? With mandatory substitutions the problem is The gross weight numof a ship is 20000 tons . If its net weight is 15000 tons , what is the weight numof the ships cargo ? The simple sentences are The gross weight numof a ship is 20000 tons . Its net weight is 15000 tons . What is the weight numof the ships cargo ? The equations to be solved are Equal [gross weight of ship] [product 20000 [tons]] Equal [its net weight] [product 15000 [tons]] The equations were insufficient to find a solution. Do you know any more relationships among these variables? Weight of ships cargo Its net weight Tons Gross weight of ship The weight of a ships cargo is the gross weight minus the net weight Assuming that [net weight] is equal to [its net weight] Assuming that [gross weight] is equal to [gross weight of ship] The weight of the ships cargo is 5000 tons The problem is solved.
Student relies on certain stereotyped forms of sentences in the problems it solves. It's easy to make up problems that will completely bewilder it:
Suppose you have 14 jelly beans. You give 2 each to Tom, Dick, and Harry. How many do you have left?
The first mistake Student makes is that it thinks the word
and following a comma separates two clauses; it generates simple sentences
You give 2 each to Tom , Dick . Harry .
This is quite a fundamental problem; Student's understanding of
the difference between a phrase and a clause is extremely primitive and
prone to error. Adding another pattern won't solve this one; the trouble
is that Student pays no attention to the words in between the key words like
and.
There are several other difficulties with this problem, some worse than
others. Student doesn't recognize the word suppose as having a
special function in the sentence, so it makes up a noun phrase suppose
you just like the russians. This could be fixed with an idiomatic
substitution that just ignored suppose. Another relatively small
problem is that the sentence starting how many doesn't say how many of
what; Student needs a way to understand that the relevant noun phrase is
jelly beans and not, for example, Tom. The words give
(representing subtraction) and each (representing counting a set and
then multiplying) have special mathematical meanings comparable to
percent less. A much more subtle problem
in knowledge representation is
that in this problem there are two different quantities that could be called
the number of jelly beans you have: the number you have at the
beginning of the problem and the number you have at the end. Student has a
limited understanding of this passage-of-time difficulty when it's doing an
age problem, but not in general.
How many more difficulties can you find in this problem? For how many of them can you invent improvements to Student to get around them?
Some difficulties seem to require a "more of the same" strategy: adding some new patterns to Student that are similar to the ones already there. Other difficulties seem to require a more fundamental redesign. Can that redesign be done using a pattern matcher as the central tool, or are more powerful tools needed? How powerful is pattern matching, anyway?
Answering questions like these is the job of automata theory. From that
point of view, the answer is that it depends exactly what you mean by
"pattern matching." The pattern matcher used in Student is equivalent
to a finite-state machine. The important thing to note about the patterns
used in Student is that they only apply predicates to one word at a time,
not to groups of words. In other words, they don't use the @
quantifier. Here is a typical student pattern:
[^ what !:in [is are] #one !:dlm]
For the purposes of this discussion, you can ignore the fact that the pattern matcher can set variables to remember which words matched each part of the pattern. In comparing a pattern matcher to a finite-state machine, the question we're asking is what categories of strings can the pattern matcher accept. This particular pattern is equivalent to the following machine:
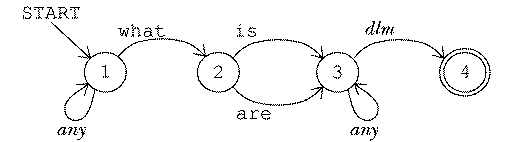
The arrow that I've labeled dlm is actually several arrows
connecting the same states, one for each symbol that the predicate dlm
accepts, i.e., period, question mark, and semicolon. Similarly, the arrows
labeled any are followed for any symbol at all. This machine is
nondeterministic, but you'll recall that that doesn't matter; we can turn it
into a deterministic one if necessary.
To be sure you understand the equivalence of patterns and finite-state machines, see if you can draw a machine equivalent to this pattern:
[I see !:in [the a an] ?:numberp &:adjective !:noun #:adverb]
This pattern uses all the quantifiers that test words one at a time.
If these patterns are equivalent to finite-state machines, you'd expect them to have trouble recognizing sentences that involve embedding of clauses within clauses, since these pose the same problem as keeping track of balancing of parentheses. For example, a sentence like "The book that the boy whom I saw yesterday was reading is interesting" would strain the capabilities of a finite-state machine. (As in the case of parentheses, we could design a FSM that could handle such sentences up to some fixed depth of embedding, but not one that could handle arbitrarily deep embedding.)
If we allow the use of the @ quantifier in patterns, and if the
predicates used to test substrings of the sentences are true functions
without side effects, then the pattern matcher is equivalent to an RTN or a
production rule grammar. What makes an RTN different from a finite-state
machine is that the former can include arrows that match several symbols
against another (or the same) RTN. Equivalently, the @ quantifier
matches several symbols against another (or the same) pattern.
A language that can be represented by an RTN is called a context-free language. The reason for the name is that in such a language a given string consistently matches or doesn't match a given predicate regardless of the rest of the sentence. That's the point of what I said just above about side effects; the output from a test predicate can't depend on anything other than its input. Pascal is a context-free language because
this := that
is always an assignment statement regardless of what other statements might be in the program with it.
What isn't a context-free language? The classic example in automata theory is the language consisting of the strings
abc aabbcc aaabbbccc aaaabbbbcccc
and so on, with the requirement that the number of as be
equal to the number of bs and also equal to the number of cs.
That language can't be represented as RTNs or production rules. (Try it.
Don't confuse it with the language that accepts any number of as
followed by any number of bs and so on; even a finite-state machine
can represent that one. The equal number requirement is important.)
The classic formal system that can represent any language for which there are precise rules is the Turing machine. Its advantage over the RTN is precisely that it can "jump around" in its memory, looking at one part while making decisions about another part.
There is a sharp theoretical boundary between context-free and context-sensitive languages, but in practice the boundary is sometimes fuzzy. Consider again the case of Pascal and that assignment statement. I said that it's recognizably an assignment statement because it matches a production rule like
assignment : identifier := expression
(along with a bunch of other rules that determine what qualifies as an expression). But that production rule doesn't really express all the requirements for a legal Pascal assignment statement. For example, the identifier and the expression must be of the same type. The actual Pascal compiler (any Pascal compiler, not just mine) includes instructions that represent the formal grammar plus extra instructions that represent the additional requirements.
The type agreement rule is an example of context sensitivity. The types of
the relevant identifiers were determined in var declarations earlier
in the program; those declarations are part of what determines whether the
given string of symbols is a legal assignment.
One could create a clean formal description of Pascal, type agreement rules and all, by designing a Turing machine to accept Pascal programs. However, Turing machines aren't easy to work with for any practical problem. It's much easier to set up a context-free grammar for Pascal and then throw in a few side effects to handle the context-sensitive aspects of the language.
Much the same is true of English. It's possible to set up an RTN (or a production rule grammar) for noun phrases, for example, and another one for verb phrases. It's tempting then to set up an RTN for a sentence like this:
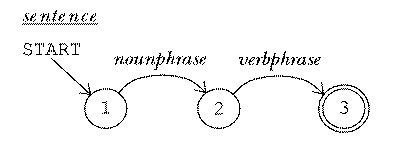
This machine captures some, but not all, of the rules of English. It's true that a sentence requires a noun phrase (the subject) and a verb phrase (the predicate). But there are agreement rules for person and number (I run but he runs) analogous to the type agreement rules of Pascal.
Some artificial intelligence researchers, understanding all this, parse
English sentences using a formal description called an
augmented transition network (ATN). An ATN is just
like an RTN except
that each transition arrow can have associated with it not only the name of
a symbol or another RTN but also some conditions that must be met in
order to follow the arrow and some actions that the program should
take if the arrow is followed. For example, we could turn the RTN just
above into an ATN by adding an action to the first arrow saying "store the
number (singular or plural) of the noun phrase in the variable
number" and adding a condition to the second arrow saying "the number of
the verb phrase must be equal to the variable number."
Subject-predicate agreement is not the only rule in English grammar best expressed as a side effect in a transition network. Below is an ATN for noun phrases taken from Language as a Cognitive Process, Volume 1: Syntax by Terry Winograd (page 598). I'm not going to attempt to explain the notation or the detailed rules here, but just to give one example, the condition labeled "h16p" says that the transition for apostrophe-s can be followed if the head of the phrase is an ordinary noun ("the book's") but not if it's a pronoun ("you's").
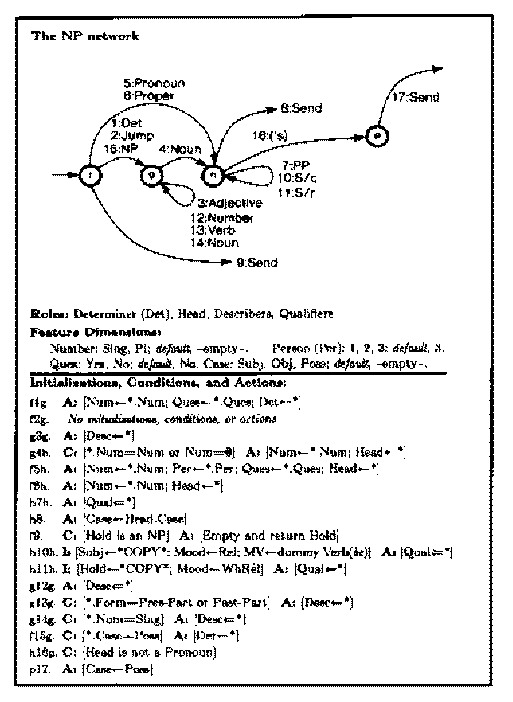
The ATN is equivalent in power to a Turing machine; there is no known mechanism that is more flexible in carrying out algorithms. The flexibility has a cost, though. The time required to parse a string with an ATN is not bounded by a polynomial function. (Remember, the time for an RTN is O(n3).) It can easily be exponential, O(2n). One reason is that a context-sensitive procedure can't be subject to memoization. If two invocations of the same procedure with the same inputs can give different results because of side effects, it does no good to remember what result we got the last time. Turning an ATN into a practical program is often possible, but not a trivial task.
In thinking about ATNs we've brought together most of the topics in this book: formal systems, algorithms, language parsing, and artificial intelligence. Perhaps that's a good place to stop.
| (back to Table of Contents) | BACK chapter thread NEXT |
to student :prob
say [The problem to be solved is] :prob
make "prob map.se [depunct ?] :prob
localmake "orgprob :prob
student1 :prob ~
[[[the perimeter of ! rectangle]
[twice the sum of the length and width of the rectangle]]
[[two numbers] [one of the numbers and the other number]]
[[two numbers] [one number and the other number]]]
end
to student1 :prob :idioms
local [simsen shelf aunits units wanted ans var lasteqn
ref eqt1 beg end idiom reply]
make "prob idioms :prob
if match [^ two numbers #] :prob ~
[make "idiom find [match (sentence "^beg first ? "#end) :orgprob] :idioms ~
tryidiom stop]
while [match [^beg the the #end] :prob] [make "prob (sentence :beg "the :end)]
say [With mandatory substitutions the problem is] :prob
ifelse match [# @:in [[as old as] [age] [years old]] #] :prob ~
[ageprob] [make "simsen bracket :prob]
lsay [The simple sentences are] :simsen
foreach [aunits wanted ans var lasteqn ref units] [make ? []]
make "shelf filter [not emptyp ?] map.se [senform ?] :simsen
lsay [The equations to be solved are] :shelf
make "units remdup :units
if trysolve :shelf :wanted :units :aunits [print [The problem is solved.] stop]
make "eqt1 remdup geteqns :var
if not emptyp :eqt1 [lsay [Using the following known relationships] :eqt1]
student2 :eqt1
end
to student2 :eqt1
make "var remdup sentence (map.se [varterms ?] :eqt1) :var
make "eqt1 sentence :eqt1 vartest :var
if not emptyp :eqt1 ~
[if trysolve (sentence :shelf :eqt1) :wanted :units :aunits
[print [The problem is solved.] stop]]
make "idiom find [match (sentence "^beg first ? "#end) :orgprob] :idioms
if not emptyp :idiom [tryidiom stop]
lsay [Do you know any more relationships among these variables?] :var
make "reply readlist
if equalp :reply [yes] [print [Tell me.] make "reply readlist]
if equalp :reply [no] [print [] print [I can't solve this problem.] stop]
make "reply map.se [depunct ?] :reply
if dlm last :reply [make "reply butlast :reply]
if not match [^beg is #end] :reply [print [I don't understand that.] stop]
make "shelf sentence :shelf :eqt1
student2 (list (list "equal opform :beg opform :end))
end
;; Mandatory substitutions
to depunct :word
if emptyp :word [output []]
if equalp first :word "$ [output sentence "$ depunct butfirst :word]
if equalp last :word "% [output sentence depunct butlast :word "percent]
if memberp last :word [. ? |;| ,] [output sentence depunct butlast :word last :word]
if emptyp butfirst :word [output :word]
if equalp last2 :word "'s [output sentence depunct butlast butlast :word "s]
output :word
end
to last2 :word
output word (last butlast :word) (last :word)
end
to idioms :sent
local "number
output changes :sent ~
[[[the sum of] ["sum]] [[square of] ["square]] [[of] ["numof]]
[[how old] ["what]] [[is equal to] ["is]]
[[years younger than] [[less than]]] [[years older than] ["plus]]
[[percent less than] ["perless]] [[less than] ["lessthan]]
[[these] ["the]] [[more than] ["plus]]
[[first two numbers] [[the first number and the second number]]]
[[three numbers]
[[the first number and the second number and the third number]]]
[[one half] [0.5]] [[twice] [[2 times]]]
[[$ !number] [sentence :number "dollars]] [[consecutive to] [[1 plus]]]
[[larger than] ["plus]] [[per cent] ["percent]] [[how many] ["howm]]
[[is multiplied by] ["ismulby]] [[is divided by] ["isdivby]]
[[multiplied by] ["times]] [[divided by] ["divby]]]
end
to changes :sent :list
localmake "keywords map.se [findkey first ?] :list
output changes1 :sent :list :keywords
end
to findkey :pattern
if equalp first :pattern "!:in [output first butfirst :pattern]
if equalp first :pattern "?:in [output sentence (item 2 :pattern) (item 3 :pattern)]
output first :pattern
end
to changes1 :sent :list :keywords
if emptyp :sent [output []]
if memberp first :sent :keywords [output changes2 :sent :list :keywords]
output fput first :sent changes1 butfirst :sent :list :keywords
end
to changes2 :sent :list :keywords
changes3 :list :list
output fput first :sent changes1 butfirst :sent :list :keywords
end
to changes3 :biglist :nowlist
if emptyp :nowlist [stop]
if changeone first :nowlist [changes3 :biglist :biglist stop]
changes3 :biglist butfirst :nowlist
end
to changeone :change
local "end
if not match (sentence first :change [#end]) :sent [output "false]
make "sent run (sentence "sentence last :change ":end)
output "true
end
;; Division into simple sentences
to bracket :prob
output bkt1 finddelim :prob
end
to finddelim :sent
output finddelim1 :sent [] []
end
to finddelim1 :in :out :simples
if emptyp :in ~
[ifelse emptyp :out [output :simples] [output lput (sentence :out ".) :simples]]
if dlm first :in ~
[output finddelim1 (nocap butfirst :in) []
(lput (sentence :out first :in) :simples)]
output finddelim1 (butfirst :in) (sentence :out first :in) :simples
end
to nocap :words
if emptyp :words [output []]
if personp first :words [output :words]
output sentence (lowercase first :words) butfirst :words
end
to bkt1 :problist
local [first word rest]
if emptyp :problist [output []]
if not memberp ", first :problist ~
[output fput first :problist bkt1 butfirst :problist]
if match [if ^first , !word:qword #rest] first :problist ~
[output bkt1 fput (sentence :first ".)
fput (sentence :word :rest) butfirst :problist]
if match [^first , and #rest] first :problist ~
[output fput (sentence :first ".) (bkt1 fput :rest butfirst :problist)]
output fput first :problist bkt1 butfirst :problist
end
;; Age problems
to ageprob
local [beg end sym who num subj ages]
while [match [^beg as old as #end] :prob] [make "prob sentence :beg :end]
while [match [^beg years old #end] :prob] [make "prob sentence :beg :end]
while [match [^beg will be when #end] :prob] ~
[make "sym gensym
make "prob (sentence :beg "in :sym [years . in] :sym "years :end)]
while [match [^beg was when #end] :prob] ~
[make "sym gensym
make "prob (sentence :beg :sym [years ago .] :sym [years ago] :end)]
while [match [^beg !who:personp will be in !num years #end] :prob] ~
[make "prob (sentence :beg :who [s age in] :num "years #end)]
while [match [^beg was #end] :prob] [make "prob (sentence :beg "is :end)]
while [match [^beg will be #end] :prob] [make "prob (sentence :beg "is :end)]
while [match [^beg !who:personp is now #end] :prob] ~
[make "prob (sentence :beg :who [s age now] :end)]
while [match [^beg !num years from now #end] :prob] ~
[make "prob (sentence :beg "in :num "years :end)]
make "prob ageify :prob
ifelse match [^ !who:personp ^end s age #] :prob ~
[make "subj sentence :who :end] [make "subj "someone]
make "prob agepron :prob
make "end :prob
make "ages []
while [match [^ !who:personp ^beg age #end] :end] ~
[push "ages (sentence "and :who :beg "age)]
make "ages butfirst reduce "sentence remdup :ages
while [match [^beg their ages #end] :prob] [make "prob (sentence :beg :ages :end)]
make "simsen map [agesen ?] bracket :prob
end
to ageify :sent
if emptyp :sent [output []]
if not personp first :sent [output fput first :sent ageify butfirst :sent]
catch "error [if equalp first butfirst :sent "s
[output fput first :sent ageify butfirst :sent]]
output (sentence first :sent [s age] ageify butfirst :sent)
end
to agepron :sent
if emptyp :sent [output []]
if not pronoun first :sent [output fput first :sent agepron butfirst :sent]
if posspro first :sent [output (sentence :subj "s agepron butfirst :sent)]
output (sentence :subj [s age] agepron butfirst :sent)
end
to agesen :sent
local [when rest num]
make "when []
if match [in !num years #rest] :sent ~
[make "when sentence "pluss :num make "sent :rest]
if match [!num years ago #rest] :sent ~
[make "when sentence "minuss :num make "sent :rest]
output agewhen :sent
end
to agewhen :sent
if emptyp :sent [output []]
if not equalp first :sent "age [output fput first :sent agewhen butfirst :sent]
if match [in !num years #rest] butfirst :sent ~
[output (sentence [age pluss] :num agewhen :rest)]
if match [!num years ago #rest] butfirst :sent ~
[output (sentence [age minuss] :num agewhen :rest)]
if equalp "now first butfirst :sent ~
[output sentence "age agewhen butfirst butfirst :sent]
output (sentence "age :when agewhen butfirst :sent)
end
;; Translation from sentences into equations
to senform :sent
make "lasteqn senform1 :sent
output :lasteqn
end
to senform1 :sent
local [one two verb1 verb2 stuff1 stuff2 factor]
if emptyp :sent [output []]
if match [^ what are ^one and ^two !:dlm] :sent ~
[output fput (qset :one) (senform (sentence [what are] :two "?))]
if match [^ what !:in [is are] #one !:dlm] :sent ~
[output (list qset :one)]
if match [^ howm !one is #two !:dlm] :sent ~
[push "aunits (list :one) output (list qset :two)]
if match [^ howm ^one do ^two have !:dlm] :sent ~
[output (list qset (sentence [the number of] :one :two "have))]
if match [^ howm ^one does ^two have !:dlm] :sent ~
[output (list qset (sentence [the number of] :one :two "has))]
if match [^ find ^one and #two] :sent ~
[output fput (qset :one) (senform sentence "find :two)]
if match [^ find #one !:dlm] :sent [output (list qset :one)]
make "sent filter [not article ?] :sent
if match [^one ismulby #two] :sent ~
[push "ref (list "product opform :one opform :two) output []]
if match [^one isdivby #two] :sent ~
[push "ref (list "quotient opform :one opform :two) output []]
if match [^one is increased by #two] :sent ~
[push "ref (list "sum opform :one opform :two) output []]
if match [^one is #two] :sent ~
[output (list (list "equal opform :one opform :two))]
if match [^one !verb1:verb ^factor as many ^stuff1 as
^two !verb2:verb ^stuff2 !:dlm] ~
:sent ~
[if emptyp :stuff2 [make "stuff2 :stuff1]
output (list (list "equal ~
opform (sentence [the number of] :stuff1 :one :verb1) ~
opform (sentence :factor [the number of] :stuff2 :two :verb2)))]
if match [^one !verb1:verb !factor:numberp #stuff1 !:dlm] :sent ~
[output (list (list "equal ~
opform (sentence [the number of] :stuff1 :one :verb1) ~
opform (list :factor)))]
say [This sentence form is not recognized:] :sent
throw "error
end
to qset :sent
localmake "opform opform filter [not article ?] :sent
if not operatorp first :opform ~
[queue "wanted :opform queue "ans list :opform oprem :sent output []]
localmake "gensym gensym
queue "wanted :gensym
queue "ans list :gensym oprem :sent
output (list "equal :gensym opform (filter [not article ?] :sent))
end
to oprem :sent
output map [ifelse equalp ? "numof ["of] [?]] :sent
end
to opform :expr
local [left right op]
if match [^left !op:op2 #right] :expr [output optest :op :left :right]
if match [^left !op:op1 #right] :expr [output optest :op :left :right]
if match [^left !op:op0 #right] :expr [output optest :op :left :right]
if match [#left !:dlm] :expr [make "expr :left]
output nmtest filter [not article ?] :expr
end
to optest :op :left :right
output run (list (word "tst. :op) :left :right)
end
to tst.numof :left :right
if numberp last :left [output (list "product opform :left opform :right)]
output opform (sentence :left "of :right)
end
to tst.divby :left :right
output (list "quotient opform :left opform :right)
end
to tst.tothepower :left :right
output (list "expt opform :left opform :right)
end
to expt :num :pow
if :pow < 1 [output 1]
output :num * expt :num :pow - 1
end
to tst.per :left :right
output (list "quotient ~
opform :left ~
opform (ifelse numberp first :right [:right] [fput 1 :right]))
end
to tst.lessthan :left :right
output opdiff opform :right opform :left
end
to opdiff :left :right
output (list "sum :left (list "minus :right))
end
to tst.minus :left :right
if emptyp :left [output list "minus opform :right]
output opdiff opform :left opform :right
end
to tst.minuss :left :right
output tst.minus :left :right
end
to tst.sum :left :right
local [one two three]
if match [^one and ^two and #three] :right ~
[output (list "sum opform :one opform (sentence "sum :two "and :three))]
if match [^one and #two] :right ~
[output (list "sum opform :one opform :two)]
say [sum used wrong:] :right
throw "error
end
to tst.squared :left :right
output list "square opform :left
end
to tst.difference :left :right
local [one two]
if match [between ^one and #two] :right [output opdiff opform :one opform :two]
say [Incorrect use of difference:] :right
throw "error
end
to tst.plus :left :right
output (list "sum opform :left opform :right)
end
to tst.pluss :left :right
output tst.plus :left :right
end
to square :x
output :x * :x
end
to tst.square :left :right
output list "square opform :right
end
to tst.percent :left :right
if not numberp last :left ~
[say [Incorrect use of percent:] :left throw "error]
output opform (sentence butlast :left ((last :left) / 100) :right)
end
to tst.perless :left :right
if not numberp last :left ~
[say [Incorrect use of percent:] :left throw "error]
output (list "product ~
(opform sentence butlast :left ((100 - (last :left)) / 100)) ~
opform :right)
end
to tst.times :left :right
if emptyp :left [say [Incorrect use of times:] :right throw "error]
output (list "product opform :left opform :right)
end
to nmtest :expr
if match [& !:numberp #] :expr [say [argument error:] :expr throw "error]
if and (equalp first :expr 1) (1 < count :expr) ~
[make "expr (sentence 1 plural (first butfirst :expr) (butfirst butfirst :expr))]
if and (numberp first :expr) (1 < count :expr) ~
[push "units (list first butfirst :expr) ~
output (list "product (first :expr) (opform butfirst :expr))]
if numberp first :expr [output first :expr]
if memberp "this :expr [output this :expr]
if not memberp :expr :var [push "var :expr]
output :expr
end
to this :expr
if not emptyp :ref [output pop "ref]
if not emptyp :lasteqn [output first butfirst last :lasteqn]
if equalp first :expr "this [make "expr butfirst :expr]
push "var :expr
output :expr
end
;; Solving the equations
to trysolve :shelf :wanted :units :aunits
local "solution
make "solution solve :wanted :shelf (ifelse emptyp :aunits [:units] [:aunits])
output pranswers :ans :solution
end
to solve :wanted :eqt :terms
output solve.reduce solver :wanted :terms [] [] "insufficient
end
to solve.reduce :soln
if emptyp :soln [output []]
if wordp :soln [output :soln]
if emptyp butfirst :soln [output :soln]
local "part
make "part solve.reduce butfirst :soln
output fput (list (first first :soln) (subord last first :soln :part)) :part
end
to solver :wanted :terms :alis :failed :err
local [one result restwant]
if emptyp :wanted [output :err]
make "one solve1 (first :wanted) ~
(sentence butfirst :wanted :failed :terms) ~
:alis :eqt [] "insufficient
if wordp :one ~
[output solver (butfirst :wanted) :terms :alis (fput first :wanted :failed) :one]
make "restwant (sentence :failed butfirst :wanted)
if emptyp :restwant [output :one]
make "result solver :restwant :terms :one [] "insufficient
if listp :result [output :result]
output solver (butfirst :wanted) :terms :alis (fput first :wanted :failed) :one
end
to solve1 :x :terms :alis :eqns :failed :err
local [thiseq vars extras xterms others result]
if emptyp :eqns [output :err]
make "thiseq subord (first :eqns) :alis
make "vars varterms :thiseq
if not memberp :x :vars ~
[output solve1 :x :terms :alis (butfirst :eqns) (fput first :eqns :failed) :err]
make "xterms fput :x :terms
make "extras setminus :vars :xterms
make "eqt remove (first :eqns) :eqt
if not emptyp :extras ~
[make "others solver :extras :xterms :alis [] "insufficient
ifelse wordp :others
[make "eqt sentence :failed :eqns
output solve1 :x :terms :alis (butfirst :eqns)
(fput first :eqns :failed) :others]
[make "alis :others
make "thiseq subord (first :eqns) :alis]]
make "result solveq :x :thiseq
if listp :result [output lput :result :alis]
make "eqt sentence :failed :eqns
output solve1 :x :terms :alis (butfirst :eqns) (fput first :eqns :failed) :result
end
to solveq :var :eqn
local [left right]
make "left first butfirst :eqn
ifelse occvar :var :left ~
[make "right last :eqn] [make "right :left make "left last :eqn]
output solveq1 :left :right "true
end
to solveq1 :left :right :bothtest
if :bothtest [if occvar :var :right [output solveqboth :left :right]]
if equalp :left :var [output list :var :right]
if wordp :left [output "unsolvable]
local "oper
make "oper first :left
if memberp :oper [sum product minus quotient] [output run (list word "solveq. :oper)]
output "unsolvable
end
to solveqboth :left :right
if not equalp first :right "sum [output solveq1 (subterm :left :right) 0 "false]
output solveq.rplus :left butfirst :right []
end
to solveq.rplus :left :right :newright
if emptyp :right [output solveq1 :left (simone "sum :newright) "false]
if occvar :var first :right ~
[output solveq.rplus (subterm :left first :right) butfirst :right :newright]
output solveq.rplus :left butfirst :right (fput first :right :newright)
end
to solveq.sum
if emptyp butfirst butfirst :left [output solveq1 first butfirst :left :right "true]
output solveq.sum1 butfirst :left :right []
end
to solveq.sum1 :left :right :newleft
if emptyp :left [output solveq.sum2]
if occvar :var first :left ~
[output solveq.sum1 butfirst :left :right fput first :left :newleft]
output solveq.sum1 butfirst :left (subterm :right first :left) :newleft
end
to solveq.sum2
if emptyp butfirst :newleft [output solveq1 first :newleft :right "true]
localmake "factor factor :newleft :var
if equalp first :factor "unknown [output "unsolvable]
if equalp last :factor 0 [output "unsolvable]
output solveq1 first :factor (divterm :right last :factor) "true
end
to solveq.minus
output solveq1 (first butfirst :left) (minusin :right) "false
end
to solveq.product
output solveq.product1 :left :right
end
to solveq.product1 :left :right
if emptyp butfirst butfirst :left [output solveq1 (first butfirst :left) :right "true]
if not occvar :var first butfirst :left ~
[output solveq.product1 (fput "product butfirst butfirst :left)
(divterm :right first butfirst :left)]
localmake "rest simone "product butfirst butfirst :left
if occvar :var :rest [output "unsolvable]
output solveq1 (first butfirst :left) (divterm :right :rest) "false
end
to solveq.quotient
if occvar :var first butfirst :left ~
[output solveq1 (first butfirst :left) (simtimes list :right last :left) "true]
output solveq1 (simtimes list :right last :left) (first butfirst :left) "true
end
to denom :fract :addends
make "addends simplus :addends
localmake "den last :fract
if not equalp first :addends "quotient ~
[output simdiv list (simone "sum
(remop "sum list (distribtimes (list :addends) :den)
first butfirst :fract))
:den]
if equalp :den last :addends ~
[output simdiv (simplus list (first butfirst :fract) (first butfirst :addends))
:den]
localmake "lowterms simdiv list :den last :addends
output simdiv list (simplus (simtimes list first butfirst :fract last :lowterms)
(simtimes list first butfirst :addends
first butfirst :lowterms)) ~
(simtimes list first butfirst :lowterms last :addends)
end
to distribtimes :trms :multiplier
output simplus map [simtimes (list ? :multiplier)] :trms
end
to distribx :expr
local [oper args]
if emptyp :expr [output :expr]
make "oper first :expr
if not operatorp :oper [output :expr]
make "args map [distribx ?] butfirst :expr
if reduce "and map [numberp ?] :args [output run (sentence [(] :oper :args [)])]
if equalp :oper "sum [output simplus :args]
if equalp :oper "minus [output minusin first :args]
if equalp :oper "product [output simtimes :args]
if equalp :oper "quotient [output simdiv :args]
output fput :oper :args
end
to divterm :dividend :divisor
if equalp :dividend 0 [output 0]
output simdiv list :dividend :divisor
end
to factor :exprs :var
local "trms
make "trms map [factor1 :var ?] :exprs
if memberp "unknown :trms [output fput "unknown :exprs]
output list :var simplus :trms
end
to factor1 :var :expr
localmake "negvar minusin :var
if equalp :var :expr [output 1]
if equalp :negvar :expr [output -1]
if emptyp :expr [output "unknown]
if equalp first :expr "product [output factor2 butfirst :expr]
if not equalp first :expr "quotient [output "unknown]
localmake "dividend first butfirst :expr
if equalp :var :dividend [output (list "quotient 1 last :expr)]
if not equalp first :dividend "product [output "unknown]
localmake "result factor2 butfirst :dividend
if equalp :result "unknown [output "unknown]
output (list "quotient :result last :expr)
end
to factor2 :trms
if memberp :var :trms [output simone "product (remove :var :trms)]
if memberp :negvar :trms [output minusin simone "product (remove :negvar :trms)]
output "unknown
end
to maybeadd :num :rest
if equalp :num 0 [output :rest]
output fput :num :rest
end
to maybemul :num :rest
if equalp :num 1 [output :rest]
output fput :num :rest
end
to minusin :expr
if emptyp :expr [output -1]
if equalp first :expr "sum [output fput "sum map [minusin ?] butfirst :expr]
if equalp first :expr "minus [output last :expr]
if memberp first :expr [product quotient] ~
[output fput first :expr
(fput (minusin first butfirst :expr) butfirst butfirst :expr)]
if numberp :expr [output minus :expr]
output list "minus :expr
end
to occvar :var :expr
if emptyp :expr [output "false]
if wordp :expr [output equalp :var :expr]
if operatorp first :expr [output not emptyp find [occvar :var ?] butfirst :expr]
output equalp :var :expr
end
to remfactor :num :den
foreach butfirst :num [remfactor1 ?]
output (list "quotient (simone "product butfirst :num) (simone "product butfirst :den))
end
to remfactor1 :expr
local "neg
if memberp :expr :den ~
[make "num remove :expr :num make "den remove :expr :den stop]
make "neg minusin :expr
if not memberp :neg :den [stop]
make "num remove :expr :num
make "den minusin remove :neg :den
end
to remop :oper :exprs
output map.se [ifelse equalp first ? :oper [butfirst ?] [(list ?)]] :exprs
end
to simdiv :list
local [num den numop denop]
make "num first :list
make "den last :list
if equalp :num :den [output 1]
if numberp :den [output simtimes (list (quotient 1 :den) :num)]
make "numop first :num
make "denop first :den
if equalp :numop "quotient ~
[output simdiv list (first butfirst :num) (simtimes list last :num :den)]
if equalp :denop "quotient ~
[output simdiv list (simtimes list :num last :den) (first butfirst :den)]
if and equalp :numop "product equalp :denop "product [output remfactor :num :den]
if and equalp :numop "product memberp :den :num [output remove :den :num]
output fput "quotient :list
end
to simone :oper :trms
if emptyp :trms [output ifelse equalp :oper "product [1] [0]]
if emptyp butfirst :trms [output first :trms]
output fput :oper :trms
end
to simplus :exprs
make "exprs remop "sum :exprs
localmake "factor [unknown]
catch "simplus ~
[foreach :terms ~
[make "factor (factor :exprs ?) ~
if not equalp first :factor "unknown [throw "simplus]]]
if not equalp first :factor "unknown [output fput "product remop "product :factor]
localmake "nums 0
localmake "nonnums []
localmake "quick []
catch "simplus [simplus1 :exprs]
if not emptyp :quick [output :quick]
if not equalp :nums 0 [push "nonnums :nums]
output simone "sum :nonnums
end
to simplus1 :exprs
if emptyp :exprs [stop]
simplus2 first :exprs
simplus1 butfirst :exprs
end
to simplus2 :pos
local "neg
make "neg minusin :pos
if numberp :pos [make "nums sum :pos :nums stop]
if memberp :neg butfirst :exprs [make "exprs remove :neg :exprs stop]
if equalp first :pos "quotient ~
[make "quick (denom :pos (maybeadd :nums sentence :nonnums butfirst :exprs)) ~
throw "simplus]
push "nonnums :pos
end
to simtimes :exprs
local [nums nonnums quick]
make "nums 1
make "nonnums []
make "quick []
catch "simtimes [foreach remop "product :exprs [simtimes1 ?]]
if not emptyp :quick [output :quick]
if equalp :nums 0 [output 0]
if not equalp :nums 1 [push "nonnums :nums]
output simone "product :nonnums
end
to simtimes1 :expr
if equalp :expr 0 [make "nums 0 throw "simtimes]
if numberp :expr [make "nums product :expr :nums stop]
if equalp first :expr "sum ~
[make "quick distribtimes (butfirst :expr)
(simone "product maybemul :nums sentence :nonnums ?rest)
throw "simtimes]
if equalp first :expr "quotient ~
[make "quick
simdiv (list (simtimes (list (first butfirst :expr)
(simone "product
maybemul :nums
sentence :nonnums ?rest)))
(last :expr))
throw "simtimes]
push "nonnums :expr
end
to subord :expr :alist
output distribx subord1 :expr :alist
end
to subord1 :expr :alist
if emptyp :alist [output :expr]
output subord (substop (last first :alist) (first first :alist) :expr) ~
(butfirst :alist)
end
to substop :val :var :expr
if emptyp :expr [output []]
if equalp :expr :var [output :val]
if not operatorp first :expr [output :expr]
output fput first :expr map [substop :val :var ?] butfirst :expr
end
to subterm :minuend :subtrahend
if equalp :minuend 0 [output minusin :subtrahend]
if equalp :minuend :subtrahend [output 0]
output simplus (list :minuend minusin :subtrahend)
end
to varterms :expr
if emptyp :expr [output []]
if numberp :expr [output []]
if wordp :expr [output (list :expr)]
if operatorp first :expr [output map.se [varterms ?] butfirst :expr]
output (list :expr)
end
;; Printing the solutions
to pranswers :ans :solution
print []
if equalp :solution "unsolvable ~
[print [Unable to solve this set of equations.] output "false]
if equalp :solution "insufficient ~
[print [The equations were insufficient to find a solution.] output "false]
localmake "gotall "true
foreach :ans [if prans ? :solution [make "gotall "false]]
if not :gotall [print [] print [Unable to solve this set of equations.]]
output :gotall
end
to prans :ans :solution
localmake "result find [equalp first ? first :ans] :solution
if emptyp :result [output "true]
print (sentence cap last :ans "is unitstring last :result)
print []
output "false
end
to unitstring :expr
if numberp :expr [output roundoff :expr]
if equalp first :expr "product ~
[output sentence (unitstring first butfirst :expr)
(reduce "sentence butfirst butfirst :expr)]
if (and (listp :expr)
(not numberp first :expr)
(not operatorp first :expr)) ~
[output (sentence 1 (singular first :expr) (butfirst :expr))]
output :expr
end
to roundoff :num
if (abs (:num - round :num)) < 0.0001 [output round :num]
output :num
end
to abs :num
output ifelse (:num < 0) [-:num] [:num]
end
;; Using known relationships
to geteqns :vars
output map.se [gprop varkey ? "eqns] :vars
end
to varkey :var
local "word
if match [number of !word #] :var [output :word]
output first :var
end
;; Assuming equality of similar variables
to vartest :vars
if emptyp :vars [output []]
local [var beg end]
make "var first :vars
output (sentence (ifelse match [^beg !:pronoun #end] :var
[vartest1 :var (sentence :beg "& :end) butfirst :vars]
[[]])
(vartest1 :var (sentence "# :var "#) butfirst :vars)
(vartest butfirst :vars))
end
to vartest1 :target :pat :vars
output map [varequal :target ?] filter [match :pat ?] :vars
end
to varequal :target :var
print []
print [Assuming that]
print (sentence (list :target) [is equal to] (list :var))
output (list "equal :target :var)
end
;; Optional substitutions
to tryidiom
make "prob (sentence :beg last :idiom :end)
while [match (sentence "^beg first :idiom "#end) :prob] ~
[make "prob (sentence :beg last :idiom :end)]
say [The problem with an idiomatic substitution is] :prob
student1 :prob (remove :idiom :idioms)
end
;; Utility procedures
to qword :word
output memberp :word [find what howm how]
end
to dlm :word
output memberp :word [. ? |;|]
end
to article :word
output memberp :word [a an the]
end
to verb :word
output memberp :word [have has get gets weigh weighs]
end
to personp :word
output memberp :word [Mary Ann Bill Tom Sally Frank father uncle]
end
to pronoun :word
output memberp :word [he she it him her they them his her its]
end
to posspro :word
output memberp :word [his her its]
end
to op0 :word
output memberp :word [pluss minuss squared tothepower per sum difference numof]
end
to op1 :word
output memberp :word [times divby square]
end
to op2 :word
output memberp :word [plus minus lessthan percent perless]
end
to operatorp :word
output memberp :word [sum minus product quotient expt square equal]
end
to plural :word
localmake "plural gprop :word "plural
if not emptyp :plural [output :plural]
if not emptyp gprop :word "sing [output :word]
if equalp last :word "s [output :word]
output word :word "s
end
to singular :word
localmake "sing gprop :word "sing
if not emptyp :sing [output :sing]
if not emptyp gprop :word "plural [output :word]
if equalp last :word "s [output butlast :word]
output :word
end
to setminus :big :little
output filter [not memberp ? :little] :big
end
to say :herald :text
print []
print :herald
print []
print :text
print []
end
to lsay :herald :text
print []
print :herald
print []
foreach :text [print cap ? print []]
end
to cap :sent
if emptyp :sent [output []]
output sentence (word uppercase first first :sent butfirst first :sent) ~
butfirst :sent
end
;; The pattern matcher
to match :pat :sen
if prematch :pat :sen [output rmatch :pat :sen]
output "false
end
to prematch :pat :sen
if emptyp :pat [output "true]
if listp first :pat [output prematch butfirst :pat :sen]
if memberp first first :pat [! @ # ^ & ?] [output prematch butfirst :pat :sen]
if emptyp :sen [output "false]
localmake "rest member first :pat :sen
if not emptyp :rest [output prematch butfirst :pat :rest]
output "false
end
to rmatch :pat :sen
local [special.var special.pred special.buffer in.list]
if or wordp :pat wordp :sen [output "false]
if emptyp :pat [output emptyp :sen]
if listp first :pat [output special fput "!: :pat :sen]
if memberp first first :pat [? # ! & @ ^] [output special :pat :sen]
if emptyp :sen [output "false]
if equalp first :pat first :sen [output rmatch butfirst :pat butfirst :sen]
output "false
end
to special :pat :sen
set.special parse.special butfirst first :pat "
output run word "match first first :pat
end
to parse.special :word :var
if emptyp :word [output list :var "always]
if equalp first :word ": [output list :var butfirst :word]
output parse.special butfirst :word word :var first :word
end
to set.special :list
make "special.var first :list
make "special.pred last :list
if emptyp :special.var [make "special.var "special.buffer]
if memberp :special.pred [in anyof] [set.in]
if not emptyp :special.pred [stop]
make "special.pred first butfirst :pat
make "pat fput first :pat butfirst butfirst :pat
end
to set.in
make "in.list first butfirst :pat
make "pat fput first :pat butfirst butfirst :pat
end
to match!
if emptyp :sen [output "false]
if not try.pred [output "false]
make :special.var first :sen
output rmatch butfirst :pat butfirst :sen
end
to match?
make :special.var []
if emptyp :sen [output rmatch butfirst :pat :sen]
if not try.pred [output rmatch butfirst :pat :sen]
make :special.var first :sen
if rmatch butfirst :pat butfirst :sen [output "true]
make :special.var []
output rmatch butfirst :pat :sen
end
to match#
make :special.var []
output #test #gather :sen
end
to #gather :sen
if emptyp :sen [output :sen]
if not try.pred [output :sen]
make :special.var lput first :sen thing :special.var
output #gather butfirst :sen
end
to #test :sen
if rmatch butfirst :pat :sen [output "true]
if emptyp thing :special.var [output "false]
output #test2 fput last thing :special.var :sen
end
to #test2 :sen
make :special.var butlast thing :special.var
output #test :sen
end
to match&
output &test match#
end
to &test :tf
if emptyp thing :special.var [output "false]
output :tf
end
to match^
make :special.var []
output ^test :sen
end
to ^test :sen
if rmatch butfirst :pat :sen [output "true]
if emptyp :sen [output "false]
if not try.pred [output "false]
make :special.var lput first :sen thing :special.var
output ^test butfirst :sen
end
to match@
make :special.var :sen
output @test []
end
to @test :sen
if @try.pred [if rmatch butfirst :pat :sen [output "true]]
if emptyp thing :special.var [output "false]
output @test2 fput last thing :special.var :sen
end
to @test2 :sen
make :special.var butlast thing :special.var
output @test :sen
end
to try.pred
if listp :special.pred [output rmatch :special.pred first :sen]
output run list :special.pred quoted first :sen
end
to quoted :thing
if listp :thing [output :thing]
output word "" :thing
end
to @try.pred
if listp :special.pred [output rmatch :special.pred thing :special.var]
output run list :special.pred thing :special.var
end
to always :x
output "true
end
to in :word
output memberp :word :in.list
end
to anyof :sen
output anyof1 :sen :in.list
end
to anyof1 :sen :pats
if emptyp :pats [output "false]
if rmatch first :pats :sen [output "true]
output anyof1 :sen butfirst :pats
end
;; Sample word problems
make "ann [Mary is twice as old as Ann was when Mary was as old as Ann is now.
If Mary is 24 years old, how old is Ann?]
make "guns [The number of soldiers the Russians have is
one half of the number of guns they have. They have 7000 guns.
How many soldiers do they have?]
make "jet [The distance from New York to Los Angeles is 3000 miles.
If the average speed of a jet plane is 600 miles per hour,
find the time it takes to travel from New York to Los Angeles by jet.]
make "nums [A number is multiplied by 6 . This product is increased by 44 .
This result is 68 . Find the number.]
make "radio [The price of a radio is $69.70.
If this price is 15 percent less than the marked price, find the marked price.]
make "sally [The sum of Sally's share of some money and Frank's share is $4.50.
Sally's share is twice Frank's. Find Frank's and Sally's share.]
make "ship [The gross weight of a ship is 20000 tons.
If its net weight is 15000 tons, what is the weight of the ships cargo?]
make "span [If 1 span is 9 inches, and 1 fathom is 6 feet,
how many spans is 1 fathom?]
make "sumtwo [The sum of two numbers is 96,
and one number is 16 larger than the other number. Find the two numbers.]
make "tom [If the number of customers Tom gets is
twice the square of 20 per cent of the number of advertisements he runs,
and the number of advertisements he runs is 45,
what is the number of customers Tom gets?]
make "uncle [Bill's father's uncle is twice as old as Bill's father.
2 years from now Bill's father will be 3 times as old as Bill.
The sum of their ages is 92 . Find Bill's age.]
;; Initial data base
pprop "distance "eqns ~
[[equal [distance] [product [speed] [time]]]
[equal [distance] [product [gas consumtion] [number of gallons of gas used]]]]
pprop "feet "eqns ~
[[equal [product 1 [feet]] [product 12 [inches]]]
[equal [product 1 [yards]] [product 3 [feet]]]]
pprop "feet "sing "foot
pprop "foot "plural "feet
pprop "gallons "eqns ~
[[equal [distance] [product [gas consumtion] [number of gallons of gas used]]]]
pprop "gas "eqns ~
[[equal [distance] [product [gas consumtion] [number of gallons of gas used]]]]
pprop "inch "plural "inches
pprop "inches "eqns [[equal [product 1 [feet]] [product 12 [inches]]]]
pprop "people "sing "person
pprop "person "plural "people
pprop "speed "eqns [[equal [distance] [product [speed] [time]]]]
pprop "time "eqns [[equal [distance] [product [speed] [time]]]]
pprop "yards "eqns [[equal [product 1 [yards]] [product 3 [feet]]]]
Brian Harvey,
bh@cs.berkeley.edu