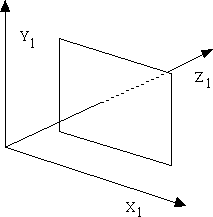
Recall the matrix for one point perspective:
_ _
| 1 0 0 0 |
P = | 0 1 0 0 |
eye | 0 0 1 1/d |
|_ 0 0 0 0 _|

Suppose we wish to view the object such that two principal axises pierce the projection plane. This two-point projection looks as follows. Note that the Z2 and X2 axises pierce the projection plane, but the Y2 axis does not.
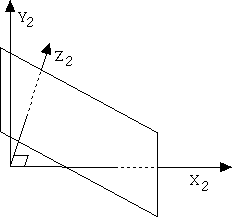
(Note on axis terminology: The number that appears after the the axis name tells us which point system we are refering to. That is, the X2 axis is the X-axis in two-point perspective coordinates. Similarily, Y1 refers to the Y-axis in one-point perspective, and Z3 will refer to the Z-axis in three-point perspective.)
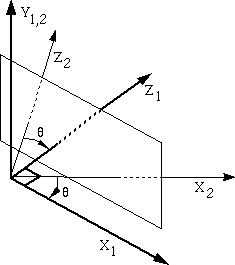
Rotating points instead of axes.
It is easier to think of this as a rotation of axes; however, in this class, we have been
assuming that we will move the points, while keeping a fixed coordinate system.
So, instead of rotating the axes by Theta, we will rotate the points by negative Theta.
Since we rotate the points back in the end, the effect will be the same.
So, we need to rotate the points through an angle negative Theta (or the axes through an angle positive Theta). In the picture below, Theta is defined positive according to the X->Y->Z->X convention. Theta is positive if it points from Z2 towards X2.
The derivation of P2
The transformation is:
(q replaces Theta because that is the letter which maps to Theta in the symbol font)
where:
_ _
| cos(q) 0 +sin(q) 0 |
R (-q) = | 0 1 0 0 |
y | -sin(q) 0 cos(q) 0 |
|_ 0 0 0 1 _|
_ _
| cos(q) 0 +sin(q) 0 |
R (-q) = | 0 1 0 0 |
y | -sin(q) 0 cos(q) 0 |
|_ 0 0 0 1 _|
When we make these substitutions:
_ _ _ _ _ _ | cos(q) 0 sin(q) 0 || 1 0 0 0 || cos(q) 0 -sin(q) 0 | | 0 1 0 0 || 0 1 0 0 || 0 1 0 1 | | -sin(q) 0 cos(q) 0 || 0 0 1 1/d || sin(q) 0 cos(q) 0 | |_ 0 0 0 1 _||_ 0 0 0 0 _||_ 0 0 0 1 _|
_ _ _ _ | cos(q) 0 sin(q) sin(q)/d || cos(q) 0 -sin(q) 0 | | 0 1 0 0 || 0 1 0 1 | | -sin(q) 0 cos(q) cos(q)/d || sin(q) 0 cos(q) 0 | |_ 0 0 0 0 _||_ 0 0 0 1 _|
_ _
| 1 0 0 sin(q)/d |
P = | 0 1 0 0 |
2 | 0 0 1 cos(q)/d |
|_ 0 0 0 0 _|
Vanishing points in two-point-projection
To illustrate the vanishing points, we can take points at infinity on the X2, Y2, and Z2, and see how they are mapped when P2 is applied. In homogeneous coordinates, a point at infinity is represented by placing zero in the W coordinate of a point vector.
So, a point at infinity on the X2 axis is represented as:
[ 1 0 0 0 ]
[ 1 0 0 sin(q)/d ]
[ d/sin(q) 0 0 ]
Similarily, the vanishing point for Z2 lies at:
[ 0 0 d/cos(q) ]
[ 0 1 0 0 ]
Note that when Theta equals zero, P2 reduces to P1.
Geometric check for two-point.
Also of note, we can verify our location of the vanishing points by using a geometric check:
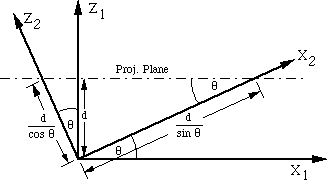
Theta is the angle between X2 and X1. Because of the projection plane is parallel to X1, the angle between the plane and X2 is also Theta. Since the sine of an angle is equal to opposite/hypotenuse (sin(theta)=opp/hyp), the length of the hypotenuse = opp/sin(Theta). opp=d, so hyp=d/sin(Theta), where hyp points along the X2 axis. This is the same as we derived for the X2 vanishing point using the matricies.
Similarily, Z2 is rotated 90 degrees from X2 and Z1 is rotated 90 degrees from X1. So, the angle between X1 and X2 is the same as the one between Z1 and Z2. cos(theta)=adjacent/hypotenuse, so hyp=adj/cos(Theta). adj=d, so hyp=d/cos(theta), and it points along Z2. This is what we derived for the Z2 vanishing point using matricies.
Now, we would also like a transformation matrix for three-point perspective. Three-point perspective occurs when three principal axes pierce the projection plane. In the following picture, X3, Y3, and Z3 all pierce the project plane.
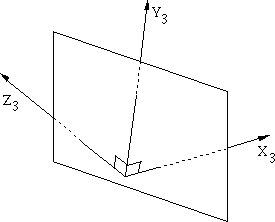
Like the two-point matrix P2, P3 can be obtained by transforming from a three-point perspective system into a one-point perpective system.
Steps to obtain a three-point perspective:
What is the three-point transformation?
Again, as with the two-point system, we need a rotation.
This particular rotation is one about X3 in the YZ plane.
If we think of rotating the coordinate axes, we rotate Y3 to Y2
by an angle -Phi about the X3 axis.
Z3 is rotated by an equal angle -Phi about X3 until it lines up
with Z2.
Note: We rotate the axes by -Phi because we are using the X->Y->Z->X rotation convention. That is, since we are rotating from Z3 towards Y3, we are rotating by a negative angle.
Because we are going to be rotating the points instead of the coordinates, we will rotate the points in the opposite direction (why?). So, when we rotate the axes by -Phi, we rotate the points by +Phi.
The point transformation matrix that we need is:
So substitution Rx into the equation for P3:
_ _
| 1 0 0 0 |
R (j) = | 0 cos(j) sin(j) 0 |
x | 0 -sin(j) cos(j) 0 |
|_ 0 0 0 1 _|
_ _ _ _n As we did in two-point projection, we will illustrate what happens to the vanishing points by applying P3 to points at infinity on the X3, Y3, and Z3 axes. As before, in homogeneous coordingates, a point at infinity is represented by placing a zero in the W coordinate of a point vector.So, a points at infinity on the X3, Y3, and Z3 axes:
become (in homogeneous coordinates): z: [ 0 0 1 0 ]eck. x: [ 1 0 0 sin(q)/d ]
Final wrap-up.
If we look at the matrix for perpective projection in three points P3:
_ _
| 1 0 0 sin(q)/d |
P = | 0 1 0 cos(q)sin(j)/d |
3 | 0 0 1 cos(q)cos(j)/d |
|_ 0 0 0 0 _|
x: [ d/sin(q) 0 0 ]
y: [ 0 d/cos(q)sin(j) 0 ]
z: [ 0 0 d/cos(q)cos(j) ]
Thus, if the projection planes intersects the X-, Y-, and Z- axes at (repectively):
[ dx 0 0 ], [ 0 dy 0 ], [ 0 0 dz ]Then the matrix for this 3-point perspective is:
_ _
| 1 0 0 1/dx |
P = | 0 1 0 1/dy |
3 | 0 0 1 1/dz |
|_ 0 0 0 0 _|
dx = dx, dy = dy, and dz = dz.
And, the 1 point and 2 point perspective matrices are special cases with 1/dx and/or 1/dy equal to zero.