A Note on the Mathematics of Two- and Three- Point Perspective

Brian A. Barsky

Review of One-point Perspective

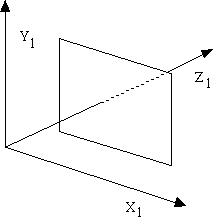
Recall the matrix for one point perspective: 

      _                   _
       |  1   0   0   0  |
P    = |  0   1   0   0  |
 eye   |  0   0   1  1/d |
       |_ 0   0   0   0 _|
This matrix projects points onto the eye-based projection plane as in the following picture. Note that only one principal axis (Z1) pierces the projection plane, so we have one-point perspective.

picture of one point projection
Figure 1: The one-point projection axes.

Two-point Perspective

Suppose we wish to view the object such that two principal axises pierce the projection plane. This two-point projection looks as follows. Note that the Z2 and X2 axises pierce the projection plane, but the Y2 axis does not.

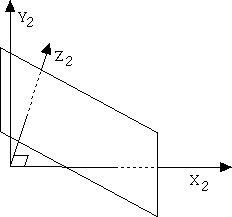
picture of two point projection
Figure 2: 1. Since we rotate about Y2, it does not move. So, Y2=Y1.

(Note on axis terminology: The number that appears after the the axis name tells us which point system we are refering to. That is, the X2 axis is the X-axis in two-point perspective coordinates. Similarily, Y1 refers to the Y-axis in one-point perspective, and Z3 will refer to the Z-axis in three-point perspective.)

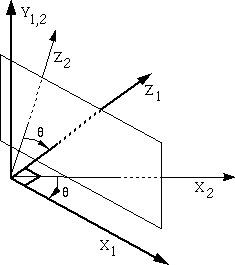
Rotating points instead of axes.

It is easier to think of this as a rotation of axes; however, in this class, we have been assuming that we will move the points, while keeping a fixed coordinate system. So, instead of rotating the axes by Theta, we will rotate the points by negative Theta. Since we rotate the points back in the end, the effect will be the same.

So, we need to rotate the points through an angle negative Theta (or the axes through an angle positive Theta). In the picture below, Theta is defined positive according to the X->Y->Z->X convention. Theta is positive if it points from Z2 towards X2.

picture of two point rotation
Figure 3: Rotation of the two-point projection axes.

The derivation of P2

The transformation is:
P2=Ry(-q)*P1*Ry(q)

(q replaces Theta because that is the letter which maps to Theta in the symbol font) where:

P1=Peye 

          _                       _
         |  cos(q)  0  +sin(q)  0  |
R (-q) = |    0     1     0     0  |
 y       | -sin(q)  0   cos(q)  0  |
         |_   0     0     0     1 _|

          _                       _
         |  cos(q)  0  +sin(q)  0  |
R (-q) = |    0     1     0     0  |
 y       | -sin(q)  0   cos(q)  0  |
         |_   0     0     0     1 _|
Note: q is substituted for Theta because at the time of creation for this document, there was no HTML theta.

When we make these substitutions: 

 _                      _  _               _  _                      _
|  cos(q)  0  sin(q)  0  ||  1   0   0   0  ||  cos(q)  0 -sin(q)  0  |
|    0     1    0     0  ||  0   1   0   0  ||    0     1    0     1  |
| -sin(q)  0  cos(q)  0  ||  0   0   1  1/d ||  sin(q)  0  cos(q)  0  |
|_   0     0    0     1 _||_ 0   0   0   0 _||_   0     0    0     1 _|

 _                            _  _                      _
|  cos(q)  0  sin(q)  sin(q)/d ||  cos(q)  0 -sin(q)  0  |
|    0     1    0         0    ||    0     1    0     1  |
| -sin(q)  0  cos(q)  cos(q)/d ||  sin(q)  0  cos(q)  0  |
|_   0     0    0         0   _||_   0     0    0     1 _|

      _                    _
     |  1   0   0 sin(q)/d  |
P  = |  0   1   0     0     |
 2   |  0   0   1 cos(q)/d  |
     |_ 0   0   0     0    _|
So, P2 is the projection transformation matrix which projects a point into a two-point projection.

Vanishing points in two-point-projection

To illustrate the vanishing points, we can take points at infinity on the X2, Y2, and Z2, and see how they are mapped when P2 is applied. In homogeneous coordinates, a point at infinity is represented by placing zero in the W coordinate of a point vector.

So, a point at infinity on the X2 axis is represented as: 

[  1   0   0   0  ]
When we apply P2 to this point, we get: 
[  1   0   0  sin(q)/d ]
In non-homogeneous coordinates, this point becomes: 
[ d/sin(q)  0   0  ]
So, the vanishing point for X2 lies at the above coordinates (in the original two-point coordinate system)

Similarily, the vanishing point for Z2 lies at: 

[  0   0   d/cos(q) ]
However, when we apply P2 to a point at infinity on Y2 we get (in homogeneous coordinates): 
[  0   1   0   0  ]
This point remains at infinity. Since we are in a two-point projection system, it makes sense that only two axes (X2 and Z2 maps to vanishing points, while one still approaches infinity.

Note that when Theta equals zero, P2 reduces to P1.

Geometric check for two-point.

Also of note, we can verify our location of the vanishing points by using a geometric check:

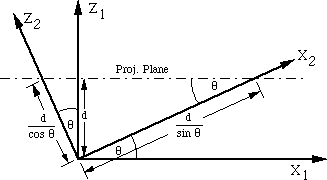
two point geometry check
Figure 4: Geometric check of P2

Theta is the angle between X2 and X1. Because of the projection plane is parallel to X1, the angle between the plane and X2 is also Theta. Since the sine of an angle is equal to opposite/hypotenuse (sin(theta)=opp/hyp), the length of the hypotenuse = opp/sin(Theta). opp=d, so hyp=d/sin(Theta), where hyp points along the X2 axis. This is the same as we derived for the X2 vanishing point using the matricies.

Similarily, Z2 is rotated 90 degrees from X2 and Z1 is rotated 90 degrees from X1. So, the angle between X1 and X2 is the same as the one between Z1 and Z2. cos(theta)=adjacent/hypotenuse, so hyp=adj/cos(Theta). adj=d, so hyp=d/cos(theta), and it points along Z2. This is what we derived for the Z2 vanishing point using matricies.

Three-point Perspective

Now, we would also like a transformation matrix for three-point perspective. Three-point perspective occurs when three principal axes pierce the projection plane. In the following picture, X3, Y3, and Z3 all pierce the project plane.

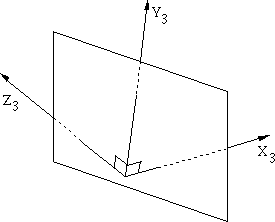
three point axis
Figure 5: The three-point projection axes

Like the two-point matrix P2, P3 can be obtained by transforming from a three-point perspective system into a one-point perpective system.

Steps to obtain a three-point perspective:

  1. transform point into 2 point system
  2. apply perspective matrix for 2 point system
  3. transform back

What is the three-point transformation?

Again, as with the two-point system, we need a rotation. This particular rotation is one about X3 in the YZ plane. If we think of rotating the coordinate axes, we rotate Y3 to Y2 by an angle -Phi about the X3 axis. Z3 is rotated by an equal angle -Phi about X3 until it lines up with Z2.

Note: We rotate the axes by -Phi because we are using the X->Y->Z->X rotation convention. That is, since we are rotating from Z3 towards Y3, we are rotating by a negative angle.

Because we are going to be rotating the points instead of the coordinates, we will rotate the points in the opposite direction (why?). So, when we rotate the axes by -Phi, we rotate the points by +Phi.

The derivation of P3

The point transformation matrix that we need is:

P3=Rx(j)*P2*Rx(-j)

(we use j instead of Phi because that is the letter used in the Symbol font)

So substitution Rx into the equation for P3: 

         _                       _
        |  1     0       0     0  |
R (j) = |  0   cos(j)  sin(j)  0  |
 x      |  0  -sin(j)  cos(j)  0  |
        |_ 0     0       0     1 _|

       _                       _  _                       _n 
As we did in two-point projection, we will illustrate what happens to the vanishing points by
applying P3 to points at infinity on the X3, Y3,
and  Z3 axes.  As before, in homogeneous coordingates, a point at infinity is represented
by placing a zero in the W coordinate of a point vector.


So, a points at infinity on the X3, Y3, and Z3 axes:


 x: [  1   0   0   0  ]


 y: [  0   1   0   0  ]


 z: [  0   0   1   0  ]

become (in homogeneous coordinates):

 x: [  1   0   0   sin(q)/d ]
eck.
Verifing X vanishing point
2 from the geometric check for two-points.

Final wrap-up.

If we look at the matrix for perpective projection in three points P3: 
       _                              _
      |   1    0    0      sin(q)/d    |
P  =  |   0    1    0   cos(q)sin(j)/d |
 3    |   0    0    1   cos(q)cos(j)/d |
      |_  0    0    0         0       _|
and compare it with the coordinates of the vanishing points in non-homogeneous coordinates: 
 x: [  d/sin(q)  0   0  ]
 y: [  0  d/cos(q)sin(j)  0  ]
 z: [  0   0   d/cos(q)cos(j) ]
we notice that the X coordinate of the X vanishing point is the inverse of the W coordinate of the X row (first row) of P3. Similarily, the Y coordinate of the Y vanishing point is the inverse of the W coordinate of the Y row (second row) of P3, and the Z coordinate of the Z vanishing point is the inverse of the W coordinate of the Z row (third row) of P3.

Thus, if the projection planes intersects the X-, Y-, and Z- axes at (repectively):

[ dx 0 0 ], [ 0 dy 0 ], [ 0 0 dz ]

Then the matrix for this 3-point perspective is: 

       _                     _
      |   1    0    0   1/dx  |
P  =  |   0    1    0   1/dy  |
 3    |   0    0    1   1/dz  |
      |_  0    0    0    0   _|
where dx = dx, dy = dy, and dz = dz.

And, the 1 point and 2 point perspective matrices are special cases with 1/dx and/or 1/dy equal to zero.

Thanks to Aaron Isaksen / EECS '98 for this html formating!