CS 284: CAGD
Texture Tiling

Texture-Mapped Subdivision Surfaces of Arbitrary Genus

The construction of a subdivision surface starts with a simple polyhedron, which is then iteratively refined and smoothed by subdivision.
The texture coordinates applied to the original polyhedron are simply subdivided in the proportion of the topological splits executed.
Problems may arise in assigning texture coordinates, if the surface is not a simple cylindical or toroidal domain.
Whenever the genus of a surface is different from 1, then you cannot regularly tile this surface with quad tile with all valence-4 vertices.
A cube has eight valence-3 vertices, and one geometrical vertex will have to carry different texture coordinates for different faces,
(thus it might be better to carry the texture coordinates with each face, rather than on a shared vertex).

To model a "spherical" ball we may start with a simple cube; but the "cubist" fish shape will extend beyond a single face and overlap into two adjacent faces.

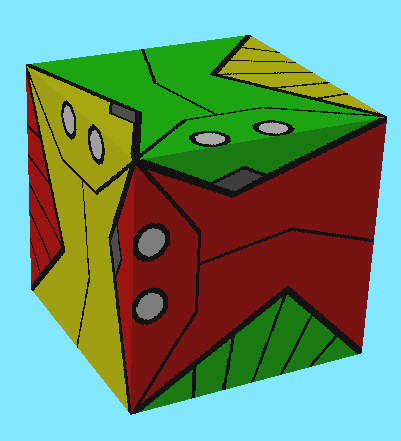
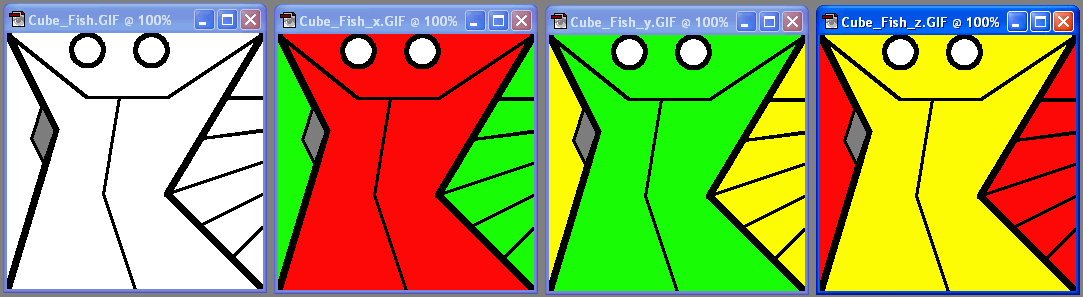
Thus the "fish" texture pattern that get's cut out by any cube face is missing the nose and the tail, but gets those two pieces stuck in from the two sides.
Since these pieces belong to some other fish, they be be of different colors; different cube faces may have different combinations of colors.
Thus, multiple copies of one B&W texture outline, filled with different colors, are needed for the different sides of the cube.
On the cube itself, the texture coordinates will then have to be rotated so that a seemless connection between the different patterns and colors occurs.
In some cases, some of the tiles may also have to be mirrored! (See the actual texture coordinates used).

Issues Arising with Texture Mapping:

What factors affect the quality of the generated texture?
How do the sizes of the triangles in the original (level 0) mesh affect the outcome of the generated texture pattern?
Can you use the "fish" tiles shown above to texture-map your mug? -- What issues might arise?

Texture-Mapping a Plane:

There is more than one way to change the tile coloring to make this possible:

Texture-Mapping a Handle Junction:

Just using the tiling patterns above is not good enough! Problems arise at the non-valence-4 corners:

We can make all four fish the same and essentially create one symmetrical super-tile that matches with itself in all orientations:

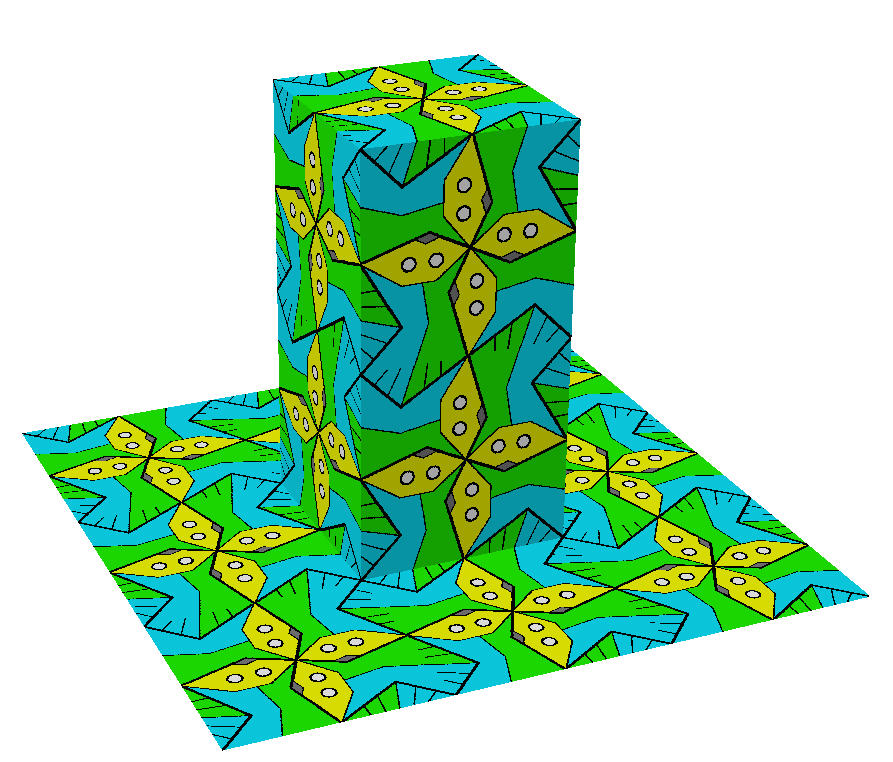
But this is not very satisfactory!

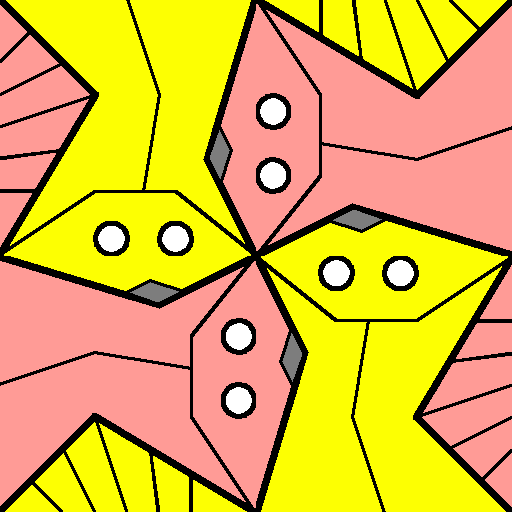
-- A more sophisticated solution introduces one more color to allow an odd number of tiles to cluster around a vertex.
This like bringing in an extra sets of (pink) strands in a weaving than needs to branch out in an area of negative Gaussian curvature:

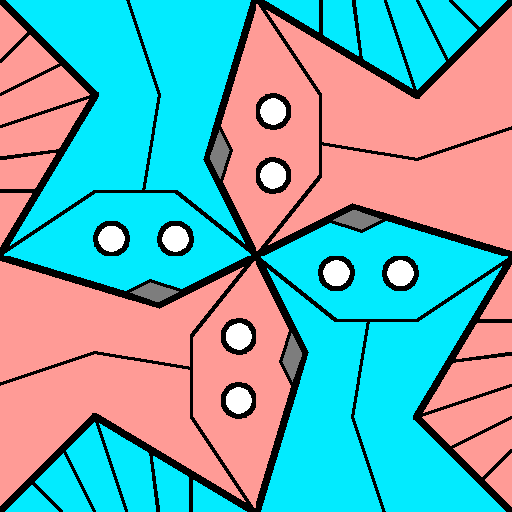
Other Tiling Systems

Example pictures of triangle tiles with different sides.
-- Again a cluster of 5 or 3 tiles can form a super-tile that can match with itself in all orientations.

- - > CS 284 HOME < - - - - > CURRENT CS284 LECTURE < - -