ABSTRACT
-----
Convolution is the main building block of convolutional neural networks (CNN). We observe that an optimized CNN often has highly correlated filters as the number of channels increases with depth, reducing the expressive power of feature representations. We propose Tied Block Convolution (TBC) that shares the same thinner filters over equal blocks of channels and produces multiple responses with a single filter. The concept of TBC can also be extended to group convolution and fully connected layers, and can be applied to various backbone networks and attention modules.
Our extensive experimentation on classification, detection, instance segmentation, and attention demonstrates TBC’s significant across-the-board gain over standard convolution and group convolution. The proposed TiedSE attention module can even use 64\(\times\) fewer parameters than the SE module to achieve comparable performance. In particular, standard CNNs often fail to accurately aggregate information in the presence of occlusion and result in multiple redundant partial object proposals. By sharing filters across channels, TBC reduces correlation and can effectively handle highly overlapping instances. TBC increases the average precision for object detection on MS-COCO by 6% when the occlusion ratio is 80%. Our code will be released.
METHOD
-----
Method overview
To generate two activation maps, standard convolution requires two full-size filters and group convolution requires two half-size filters, however, our tied block convolution only requires one half-size filter, that is, the parameters are reduced by 4\(\times\). The idea of TBC can also be applied to fully connected and group convolutional layers.
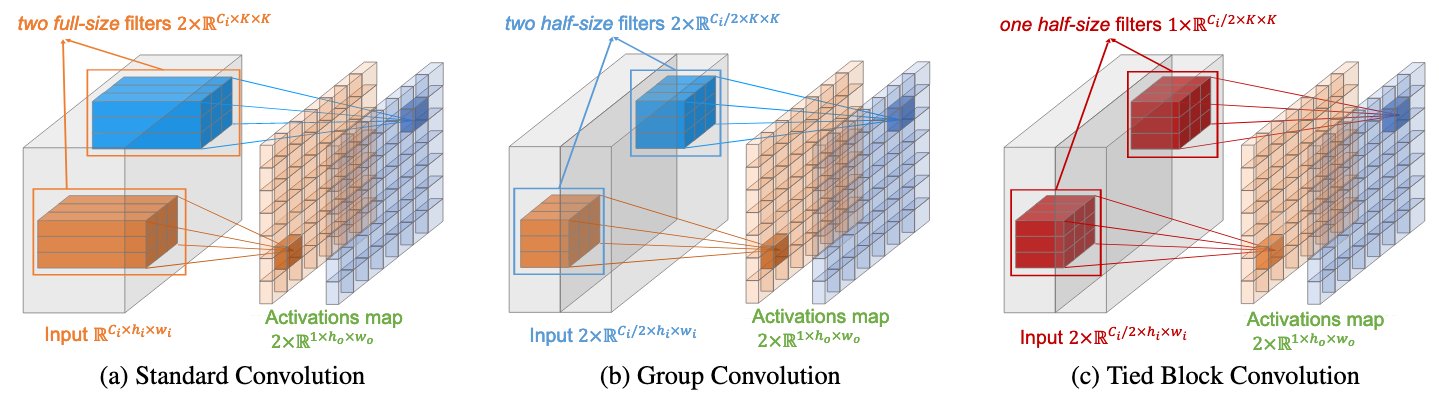
Fig 1. Standard Conv vs. Group Conv vs. Tied Block Conv
Standard Convolution
Let the input feature be denoted by \(X \in \mathbb{R}^{c_i\times h_i\times w_i}\) and the output feature \(\tilde{X} \in \mathbb{R}^{{c_o\times h_o\times w_o}}\), where \(c, h, w\) are the number of channels, the height and width of feature maps respectively. The kernel size is \(k \times k\) and the bias term is ignored for clarity. Standard Convolution, denoted by \(*\), can be formulated as:
$$ {\tilde{X} = X * W} $$where \(W \in \mathbb{R}^{c_o \times c_i \times k \times k}\) is the SC kernel. The parameters for SC is thus: \(c_o \times c_i \times k \times k.\)
Group Convolution
Group Convolution first divides input feature \(X\) into \(G\) equal-sized groups \(X_1,...,X_G\) with size \({c_i/G \times h_i \times w_i}\) per group. Each group shares the same convolutional filters \(W_g\). The output of GC is computed as:
$${ \tilde{X} = X_1 * W_1 \oplus X_2 * W_2 \oplus \cdots \oplus X_G * W_G }$$where \(\oplus\) is the concatenation operation along the channel dimension, \(W_g\) is the convolution filters for group \(g\), where \(g \in \{1,\ldots, G\}\), \(W_g\in \mathbb{R}^{\frac{c_o}{G} \times \frac{c_i}{G} \times k \times k}\). The number of parameters for GC is: \(G \times \frac{c_o}{G} \times \frac{c_i}{G} \times k \times k.\)
Tied Block Convolution (TBC)
Tied Block Convolution reduces the effective number of filters by reusing filters across different feature groups with the following formula:
$${ \tilde{X} = X_1 * W' \oplus X_2 * W' \oplus \cdots \oplus X_B * W' }$$where \(W' \in \mathbb{R}^{\frac{c_o}{B} \times \frac{c_i}{B} \times k \times k}\) is the TBC filters shared among all the groups. The parameter number is: \(\frac{c_o}{B} \times \frac{c_i}{B} \times k \times k.\)
Tied Block Group Convolution (TGC)
The idea of tied block filtering can also be directly applied to group convolution, formulated as:
$${ \tilde{X} = (X_{11} * W'_1 \oplus \cdots \oplus X_{1B} * W'_1) \oplus \cdots \oplus (X_{G1} * W'_G \oplus \cdots \oplus X_{GB} * W'_G) }$$where \(W'_g \in \mathbb{R}^{\frac{c_o}{BG} \times \frac{c_i}{BG} \times k \times k}\), \(X_{gb} \in \mathbb{R}^{\frac{c_i}{BG} \times h_i \times w_i}\) is the divided feature map, \(g \in [1, G]\) and \(b \in [1, B]\).
Tied Block Fully Connected Layer (TFC)
Convolution is a special case of fully connected (FC) layer, just as FC is a special case of convolution. We apply the same tied block filtering idea to FC. Tied block fully connected layer (TFC) shares the FC connections between equal blocks of input channels. Like TBC, TFC could reduce \(B^2\) times parameters and \(B\) times computational cost.
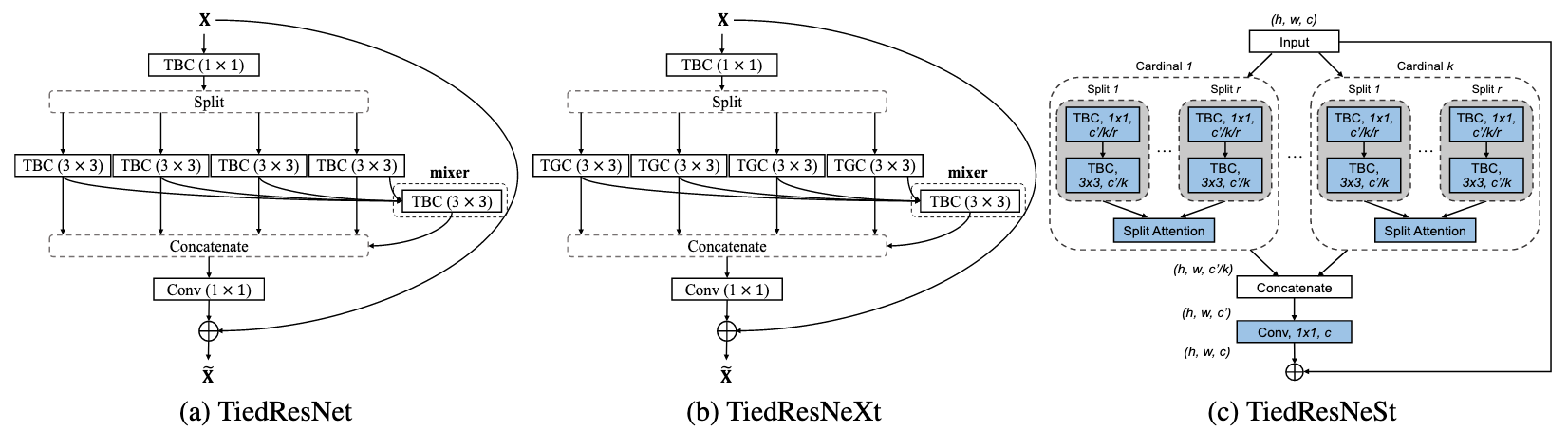
Fig 2. Diagram of bottleneck modules for (a) TiedResNet with 4 splits (b) TiedResNeXt with 4 splits and (c) TiedResNeSt. Each tied block convolution (TBC) and tied block group convolution (TGC) has a specific block number.
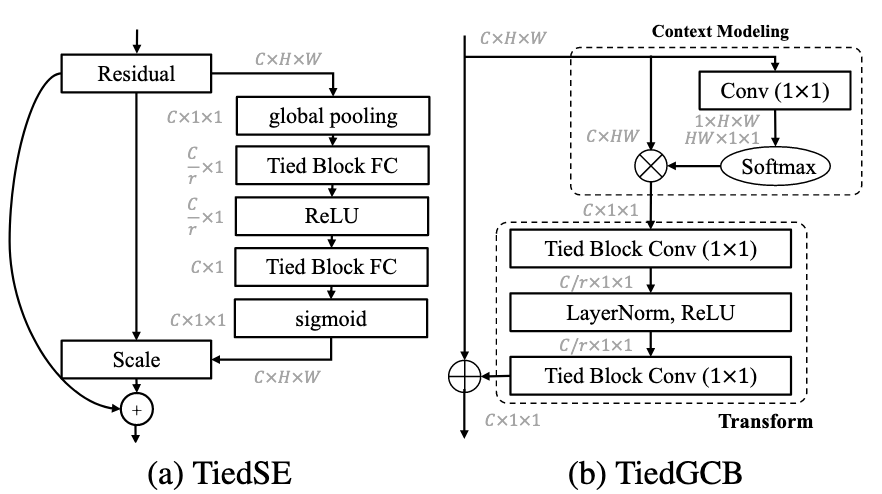
Fig 3. Diagram of Tied attention modules. (a) TiedSEmodule replaces FC in the original squeeze-and-excitation (SE) module to be TFC. (b) TiedGCB module replaces standard convolution in global context block (GCB) with TBC.
Results
-----
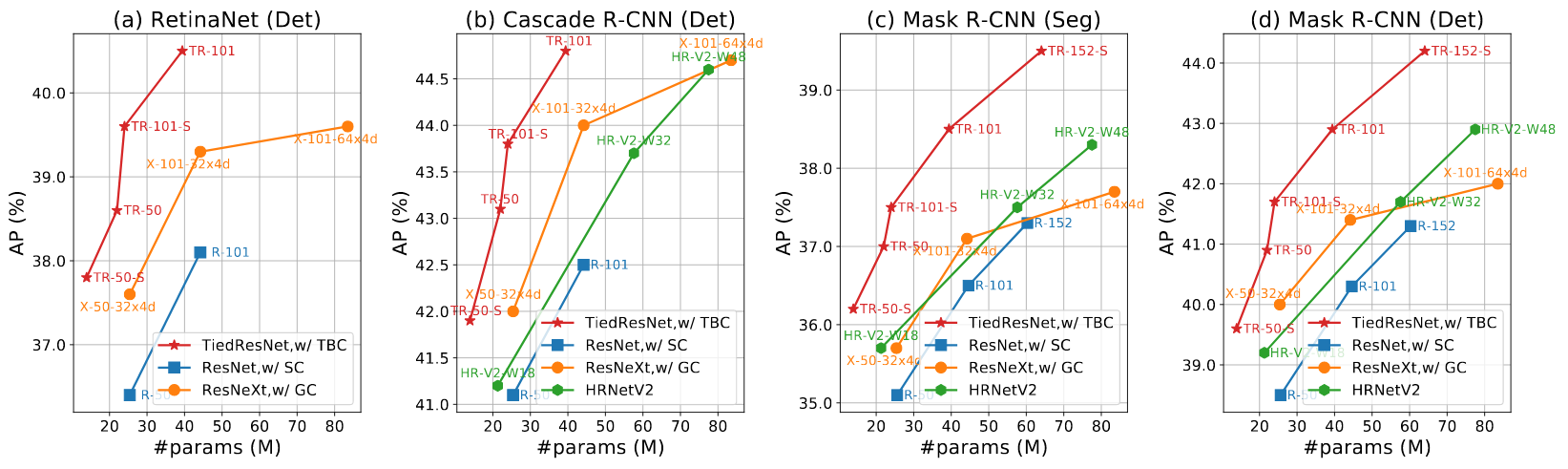
Fig 4. #params of backbones vs. their Average Precision on object detection and instance segmentation tasks of MS-COCO val-2017.
Fig 5. We evaluate TiedResNet and ResNet performance on object detection task of MS-COCO with different occlusion ratio \(r\).
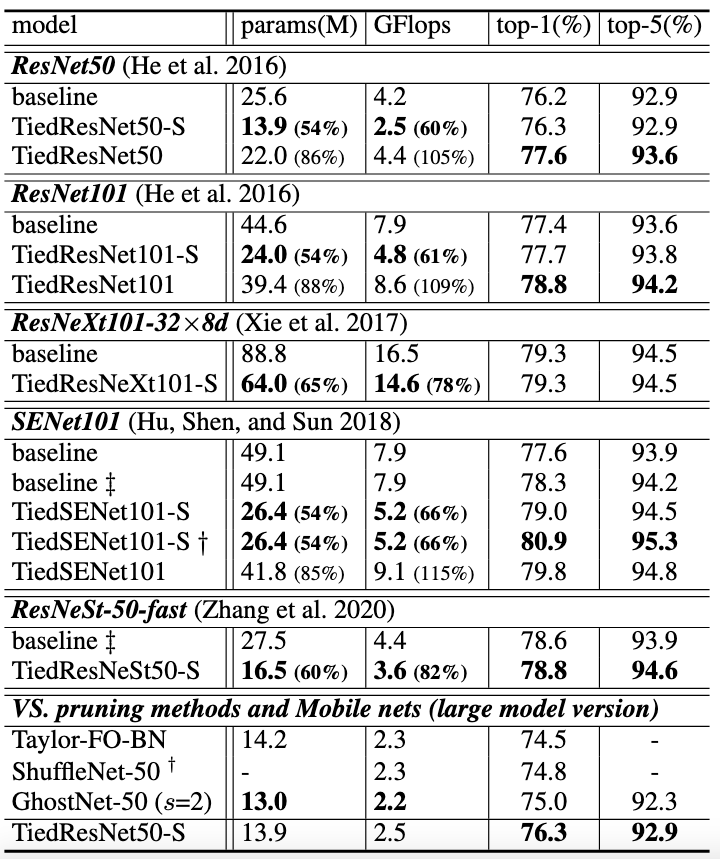
Fig 6. Recognition accuracy and model size comparison on ImageNet-1k.
Fig 7. Comparison on instance segmentation task of Cityscapes val set.
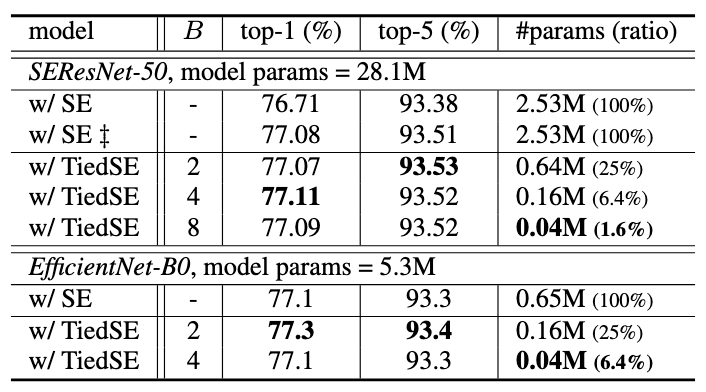
Fig 8. Comparison on #params of attention module SE/TiedSE with various backbones.
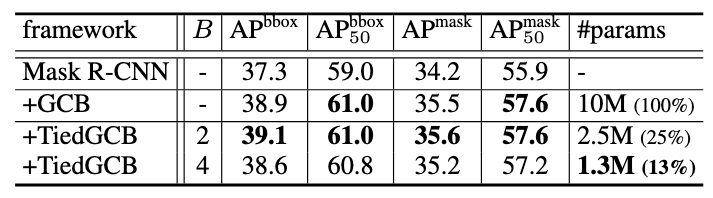
Fig 9. Comparison on #params of attention module GCB/TiedGCB.
Fig 10. Additional Grad-CAM visualization comparison among ResNet50, ResNeXt50 and TiedRes-Net50 in Rows 2-4 respectively for images in Row 1.
-----
PUBLICATION
-----
Tied Block Convolution: Leaner and Better CNNs with Shared Thinner Filters
Xudong Wang and Stella X. Yu
The Thirty-Fifth AAAI Conference on Artificial Intelligence (AAAI), 2021.
CITATION
-----
@article{wang2020unsupervised,
title={Tied Block Convolution: Leaner and Better CNNs with Shared Thinner Filters},
author={Wang, Xudong and Yu, Stella X},
journal={arXiv preprint arXiv:2009.12021},
year={2020}
}