


Next: Conclusion
Up: A
radial cumulative similarity Previous: Finding
correspondences
Results
Figure 5: Fingertip feature locations
(a) feature A, (b) feature B, (c) features C (top) and D (bottom). Feature
D is a distractor. (d-g) Raw color values and RCS transform for features
A-D. (h) Correspondence values between features for three different metrics:
L2 on intensity, robust norm (Lorentzian 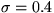 )
on intensity, and L2 on the RCS transform. The ideal
correspondence values would be near 0 for pairs of fingertips, and near
1 for pairs with the distractor. Values are not normalized and so can only
be compared within-method.
)
on intensity, and L2 on the RCS transform. The ideal
correspondence values would be near 0 for pairs of fingertips, and near
1 for pairs with the distractor. Values are not normalized and so can only
be compared within-method.
(a) (b) (b) (c) (c) (d)
(d)  (e) (e)  (f) (f)  (g) (g) 
|
Figure 5(h): Correspondence
values between features for three different metrics: L2
on intensity, robust norm (Lorentzian 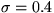 )
on intensity, and L2 on the RCS transform. The ideal
correspondence values would be near 0 for pairs of fingertips, and near
1 for pairs with the distractor. Values are not normalized and so can only
be compared within-method.
)
on intensity, and L2 on the RCS transform. The ideal
correspondence values would be near 0 for pairs of fingertips, and near
1 for pairs with the distractor. Values are not normalized and so can only
be compared within-method.
| |
A:B |
A:C |
B:C |
A:D |
B:D |
C:D |
| L2 |
0.05 |
0.35 |
0.33 |
0.27 |
0.22 |
0.15 |
| ROBUST |
0.04 |
0.62 |
0.65 |
0.38 |
0.37 |
0.20 |
| RCS |
0.05 |
0.11 |
0.07 |
0.35 |
0.27 |
0.30 |
| (ideal) |
|
|
|
1 |
1 |
1 |
Figure 6: Results of exhaustive
correspondence search for 16 different features in various image pairs.
(a,b) hand-labeled feature locations an image pair with moving eyeballs,
(f,g), an image pair with changing mouth expression. For each feature in
the first image (a,f), we searched for the point in the second image (b,g)
with minimum correspondence error using three different distance metrics:
L2, robust norm, and RCS. (c,h) Results using L2
norm on intensity, showing arrows where incorrect correspondences were
returned. There were 8 and 6 correspondence errors, with mean squared coordinate
error of 6.1 and 3.4 pixels, respectively. (d,i) Results using robust norm
on intensity: 6 and 6 correspondence errors, mean squared coordinate error
of 5.0 and 3.3 pixels. (e,j) Results using L2 norm on
RCS transform: 3 and 2 correspondence errors, mean squared coordinate error
of 2.3 and 0.4 pixels.
(a) (b) (b) (c)
(c)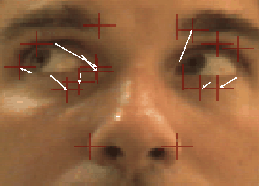 (d) (d)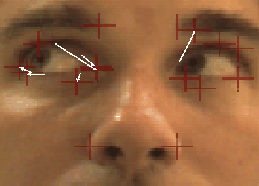 (e) (e)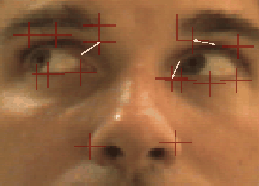 L2, 8 errors robust norm, 6 errors RCS, 3 errors
(f)
L2, 8 errors robust norm, 6 errors RCS, 3 errors
(f) (g) (g) (h)
(h) (i) (i) (j) (j) L2, 6 errors robust norm, 6 errors RCS, 2 errors
L2, 6 errors robust norm, 6 errors RCS, 2 errors
|
Figure 7: Results as in previous
figure on an image pair with a hand moving over different backgrounds.
(a) shows first image of pair, (b) results on second image using robust
norm (L2 norm yielded same result): 4 errors, mse=7.3
pixels, (c) RCS result: 2 errors, mse=0.21 pixels.
(a) (b) (b) (c) (c) |
In the present implementation we recompute all 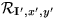 each time D is evaluated. We have not optimized for speed; using
Mn=8, Mw=50, Mc=0
a substantial fraction of a second is consumed to find a correspondence
minima per feature. However since RCS is a transform, we could easily precompute
each time D is evaluated. We have not optimized for speed; using
Mn=8, Mw=50, Mc=0
a substantial fraction of a second is consumed to find a correspondence
minima per feature. However since RCS is a transform, we could easily precompute 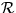 over the entire image and then be faced with the run-time cost of a standard
least-squares template search with template radius Mn
and search radius Mw.
over the entire image and then be faced with the run-time cost of a standard
least-squares template search with template radius Mn
and search radius Mw.
We compared our method to correspondence search using classic L2
norms, using normalized correlation, using a robust redescending norm (from
[1], a Lorentzian 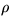 with
with 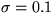 ),
and using our RCS transform with
),
and using our RCS transform with 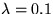 .
The L2 norm and normalized correlation yielded substantially
similar results, and so for brevity we only show L2 results
here.
.
The L2 norm and normalized correlation yielded substantially
similar results, and so for brevity we only show L2 results
here.
First we note that in the majority of image locations, all three methods
yield accurate results. It is only at points near discontinuities, and
further at points where the discontinuity changes contrast sign between
images, that there is a dramatic difference between RCS and the comparison
methods. We will thus demonstrate performance in a disproportionate number
of these cases (these are often critical locations for image analysis/synthesis
tasks).
Figure 5 shows a comparison of correspondence
values for a fingertip at various background locations (A,B,C), and a distractor
region (D) of the hand. The table in Figure 5(h)
shows that only the RCS method has correct performance: low distance measures
for all the cases of correspondence between actual fingertips (A:B, A:C,
B:C) and high distance for cases with the distractor (A:D, B:D, C:D).
Figures 6 and 7
show results from tracking 16 features simultaneously on image pairs of
an eye, mouth, and fingers, and from comparing to hand-labeled ground truth.
The mean coordinate error across the three images was 5.6 pixels for the
L2 norm, 5.2 pixels for the redescending robust norm,
and 0.97 pixels for the RCS method. The images were processed at 320x240
resolution. As expected, the L2 norm had difficulty at
regions where substantial occlusion was present, and the redescending robust
norm had problems where the designated correspondence was at a region of
occlusion contrast sign reversal. At points where no occlusion was present
the L2 and redescending norm had no coordinate error,
but the RCS did return erroneous correspondences in approximately 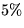 of points.
of points.
This lower performance of RCS away from occlusion boundaries is not
surprising: When analyzing an image window of a single surface where brightness
constancy holds (e.g., there is no occlusion) suboptimal performance results
from downweighting portions of the window that are actually foreground.
Informally, regions of high contrast that are prone to aliasing in the
RCS representation can be detected by computing the sum of the radial cumulative
similarity function, N: if that sum is below a certain threshold
the RCS transform should be considered degenerate. Fortunately, occlusion-free
regions of high contrast are cases where the traditional methods perform
exceedingly well. We are currently implementing a hybrid algorithm which
reverts to a L2 when that method yields good results.
Alternatively a smoothing or regularization stage would also greatly alleviate
this problem.



Next: Conclusion
Up: A
radial cumulative similarity Previous: Finding
correspondences
Trevor Darrell
9/9/1998
![]() with
with ![]() ),
and using our RCS transform with
),
and using our RCS transform with ![]() .
The L2 norm and normalized correlation yielded substantially
similar results, and so for brevity we only show L2 results
here.
.
The L2 norm and normalized correlation yielded substantially
similar results, and so for brevity we only show L2 results
here.
![]() of points.
of points.