CS 39R: Symmetry & Topology
Lecture #5 -- Mon. 10/2, 2017.

PREVIOUS <- - - - > CS 39R HOME < - - - - > CURRENT < - - - - > NEXT

Preparation:

Fill in the blanks in the Work-sheet on Surface Classification

Warm-up:

What is the genus of the following handle-bodies:
-- A hollow thick sphere with 17 tunnels through its thick shell ?
-- A hollow sphere-shell with 17 internal spokes converging at its centroid ?
-- A cube frame with 8 diagonal spokes connecting the cube vertices to the centroid ?
-- A fully connected graph with thick tubular edges connecting 6 nodes ?
-- and the following depicted objects:

(tetrahedral symmetry) (12 4th-order saddles in loop) (24 monkey-saddles in trefoil)

When you are done, look at some other models (on the table) and practice your skills in finding symmetry axes
and determining the genus of these geometrical shapes.

This is hard work! Many confusing issues!
What is the connection between Genus and Euler Characteristic?
Let's relax and form some simple but very important 2-manifolds that show some crucial differences in their parameters.

The different universes of 2D video games:

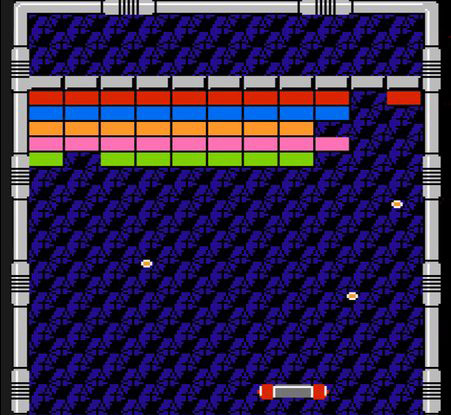
What happens to rockets or bullets that drift off to the perimeter of the screen?
How do the screens wrap around and connect to themselves?

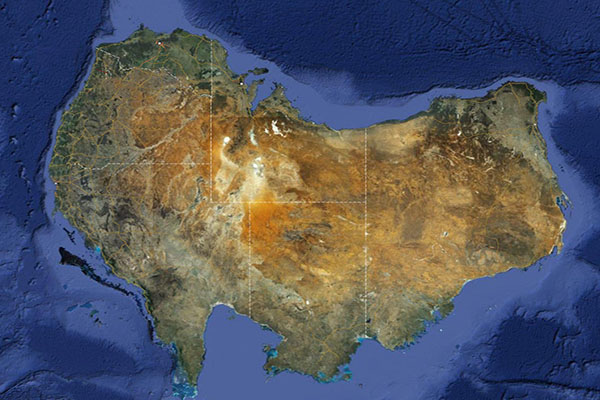
What might be the 2-manifold topology of the 2D-universe surrounding this island?
Discuss possible connectivities ("around the back-side") of this world.

Think of all possible (2-manifold) universes
that can be formed by connecting the edges
of a rectangle in different ways,
i.e., by identifying pairs of points on them
(assuming them to be connected).

Constructing simple topological 2-manifolds, -- orientable and non-orientable: PPT

Cylinders, Tori, Möbius bands, Klein bottles, Boy surface ...
They all have different surface classifications!

Surface Classification (continued)

For the topological classification of a 2-manifold, we need to count its border-loops, determine its sidedness,
and calculate its genus. The last task is the hardest one.
Often it can be solved most easily by calculating the Euler characteristic.

Euler Characteristic and Genus: PPT

Back to the Warm-up problems ...
A little bit of Graph Theory: "nodes" and "edges"
Make tree-like graphs without loops. How many edges do we need to cut to get there?
A final tree with n vertices has how many edges?

This should now allow you to calculate the genus of even very complicated 2-manifolds.

New Homework Assignment:

Due: October 9, 2017

1.) Fill in the blanks in a new Work-sheet on Surface Classification ==> "Learning by doing" !!

Some hints: The 4 structures in the bottom row are all basically a (twisting) ribbon knotted into a trefoil knot,
with some additional connections added.
In the pink trefoil the added connections are "twisting the other way" from the way they do in the grey trefoil.

E-mail me your solutions before 9am, Monday, October 9, 2017.

2.) Construct a physical model of a single-sided surface of genus 2 (e.g., using paper strips),
and then draw onto this surface two closed loops that together still leave the surface fully connected (just ONE domain).

Bring this model to class on Monday, October 9, 2017.