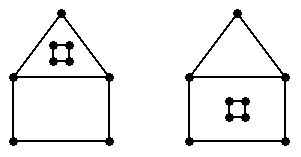
Figure 1: Two PSLGs which are topologically different if we consider the 2-faces to be part of the topology.
This is an open-book exam. It is due at the start of class on Tuesday, November 2, 1999. You may submit your answers by email, by hand, or under my office door. Answers submitted after 2:15 pm Tuesday will not be accepted. You may consult papers and other references, but you may not receive assistance from other people (except me). You are welcome to ask me to clarify anything in the readings, the lectures, or this exam that you don't fully understand.
There are 30 points worth of questions below. Answer exactly 20 points worth. If you answer questions totalling more than 20 points, I will randomly select answers to ignore, bringing the total down to 20 points. If I ignore a question that you answered correctly and grade one that you got wrong, tough luck.
[1] The quad-edge data structure (1 point). Figure 1 illustrates two PSLGs. If we consider the 2-faces to be part of each complex, then these PSLGs are topologically distinct. If we represent each PSLG with a quad-edge data structure, how do the two representations differ topologically? (In other words, if we aren't allowed to look at the coordinates of the vertices, how can we distinguish the two representations from each other?)

[2] Deloopsy (1 point). What's wrong with the following algorithm for constructing the constrained Delaunay triangulation of a simple polygon?
DELOOPSY(P)
1 while P has more than three vertices
2 Find three consecutive vertices a, b, and c on the
perimeter of P such that 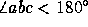 and the
circumcircle of
and the
circumcircle of 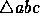 is smaller than that of
any other corner of P
3 Output
is smaller than that of
any other corner of P
3 Output 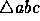 4 Splice b out of the perimeter of P
4 Splice b out of the perimeter of P
(Unfortunately, this algorithm has made an appearance in the literature.)
[3] An upper bound on two-dimensional triangulations I (1 point).
In Lecture 4,
I gave a proof that a d-dimensional triangulation of n vertices
has at most ![]() d-simplices.
(My transparencies can be viewed from the course web page).
Show how the proof method I demonstrated in class can also be used to prove
an upper bound of 2n - 5 in two dimensions. (This bound is tight.)
d-simplices.
(My transparencies can be viewed from the course web page).
Show how the proof method I demonstrated in class can also be used to prove
an upper bound of 2n - 5 in two dimensions. (This bound is tight.)
[4] An upper bound on two-dimensional triangulations II (1 point).
Show how the same proof method can also be used to show
that the bound is tight.
(In other words, a triangulation with 2n - 5 triangles exists for any
![]() .)
.)
[5] Gift-wrapping gaffes (1 point). If the gift-wrapping algorithm is used to construct the Delaunay tetrahedralization of a vertex set that includes groups of five or more cospherical vertices, the algorithm must perform checks to make sure that overlapping tetrahedra are not constructed. Even if these checks are made, if groups of six or more cospherical vertices are present, it may be possible for the algorithm to get stuck and fail to construct a valid triangulation. Explain why.
[6] Fast times with Frankensimplex (1 point).
Dr. Frankensimplex claims to have discovered an
![]() time mesh generation algorithm
that tetrahedralizes any n-vertex polyhedron so that
at least half the tetrahedra are equilateral.
Prove that the good doctor is lying.
time mesh generation algorithm
that tetrahedralizes any n-vertex polyhedron so that
at least half the tetrahedra are equilateral.
Prove that the good doctor is lying.
[7] Who needs transformations most? (2 points.) Let A and B be two bad tetrahedral meshes. Mesh A was created by applying the advancing front method to a cube. Three adjacent sides of the cube were subdivided into very small triangles, and the other three sides were subdivided into very large triangles. No background mesh or other method was used to control the sizes of the tetrahedra as the fronts advanced; rather, node placement was based only on the desire to create tetrahedra as close to equilateral as possible, until the fronts collided.
Mesh B was created by applying Shephard and Georges' Finite Octree algorithm to a domain with complicated boundaries. Each boundary octant was triangulated separately (using a Delaunay triangulation where possible), and no postprocessing was applied to improve the tetrahedra that were created where the boundaries meet the octree.
Fortunately, you have in your possession software that applies optimization-based smoothing and topological transformations (2-3 flips, edge removal, edge contraction, vertex insertion, etc.) to tetrahedral meshes. Unfortunately, the software is extremely slow, and you will only have time to apply topological transformations and smoothing to one of the two meshes. The other mesh will have to get by with smoothing alone.
Which mesh (A or B) has problems that need topological transformations to fix, and which mesh can probably heal most of its bad tetrahedra through smoothing alone? Explain why.
[8] Meshing prespecified boundaries (2 points). Assume that you are given a two-dimensional domain boundary that has been subdivided into edges, and you are not allowed to add, remove, or smooth boundary vertices. You are asked to triangulate the domain with the best-quality triangles the boundary will allow. Of the Delaunay, advancing front, and quadtree approaches, which is best suited and which is least suited to this demand? Why?
[9] Minimum spanning trees (2 points). Let V be a set of n points in the plane. The Euclidean minimum spanning tree T of V is a set of n - 1 edges such that (V, T) is a connected graph--any two vertices of V are joined by exactly one path through T--and the total length of the edges of T is shorter than (or at least as short as) that of any other spanning tree.
Prove that every edge of T is in the Delaunay triangulation of V. Hint: If (v, w) is an edge in T, but vw is not Delaunay, show that you can improve T.
[10] Constrained mesh smoothing (2 points). The optimization-based smoothing algorithm for tetrahedral meshes described by Freitag and Ollivier-Gooch chooses a search direction g. It then performs a line search along g, attempting to improve the worst dihedral angle of the tetrahedra adjoining the vertex being smoothed.
Suppose that we want to modify the algorithm so that it can smooth a vertex that is constrained to lie in a planar boundary facet. Our method is to find the orthogonal projection of g onto the facet, then use the projected search vector as our search direction.
Explain why this idea works well when there is only one angle in the active set, but is a rotten idea when there are two or more angles in the active set. Suggest a very simple fix.
[11] Off-center subsegment splitting (2 points). Ruppert's Delaunay refinement algorithm normally splits encroached subsegments at their midpoints. However, as one student pointed out in class, we might achieve smaller meshes if we use off-center splits in cases where the encroaching vertex is an input vertex (and hence can't be rejected) and is not at the subsegment's center.
For example, suppose that s is a subsegment encroached upon by an input vertex v. If v is very close to s, but not near the center of s, then splitting s off-center might reduce the number of triangles in the final mesh. One idea is to project v orthogonally onto s. Unfortunately, if v is near an endpoint of s, this idea might create an unreasonably tiny new feature, as Figure 2 illustrates.
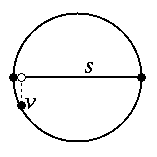
How can we modify this idea so that the termination guarantee and edge length guarantee given by Theorem 20 in the lecture notes remain intact? Be sure to use only local criteria in deciding where to place the splitting point (and not global criteria, like the value of lfsmin). Explain why Theorem 20 remains true.
[12] Herbert's typo (2 points). In Herbert Edelsbrunner's course handout, Preserving Topology, he states that the contraction of an edge ab is a local unfolding if and only if the following conditions are true.
Demonstrate why I was so confused by giving an example of a local unfolding for which condition (ii') is not satisfied.
[13] Delaunay triangulation of an x-monotone chain (4 points).
Let V = {v1, v2, ...,
vn} be a set of vertices
sorted in increasing order by x-coordinate,
with no two vertices having the same x-coordinate.
Suppose that each edge vivi + 1,
![]() ,
is known to be Delaunay.
These edges form an x-monotone chain of Delaunay edges.
,
is known to be Delaunay.
These edges form an x-monotone chain of Delaunay edges.
Consider the following ![]() algorithm
for finding the Delaunay triangulation above the chain.
(If we rotate the plane 180o,
it can triangulate the lower portion as well.)
The algorithm moves a horizontal sweepline upward over the plane,
creating each Delaunay triangle as the sweepline passes over its circumcenter.
A priority queue Q maintains a list of potential Delaunay triangles,
some of which will prove to be Delaunay, and some of which will not.
Assume that V is represented as a doubly-linked list.
algorithm
for finding the Delaunay triangulation above the chain.
(If we rotate the plane 180o,
it can triangulate the lower portion as well.)
The algorithm moves a horizontal sweepline upward over the plane,
creating each Delaunay triangle as the sweepline passes over its circumcenter.
A priority queue Q maintains a list of potential Delaunay triangles,
some of which will prove to be Delaunay, and some of which will not.
Assume that V is represented as a doubly-linked list.
TRIANGULATECHAINTOP(V) 1Prove the correctness of this algorithm. Some hints:an empty priority queue 2 for
to n - 2 3 if
,
, and
are in counterclockwise order 4 Let p be the circumcenter of
5 Insert
in Q with key p 6 while Q is not empty 7 Remove triangle
whose circumcenter has least y-coordinate from Q 8 if each edge bc and cd still has no triangle above it 9 Output
10 Splice c out of V 11 If some vertex a precedes b in V and a, b, and d are in counterclockwise order 12 Let p be the circumcenter of
13 Insert
in Q with key p 14 If some vertex e follows d in V and b, d, and e are in counterclockwise order 15 Let p be the circumcenter of
16 Insert
in Q with key p
The significance of this algorithm is that it generalizes easily to
terrains in three dimensions, or their analogues in higher dimensions,
while maintaining its ![]() running time.
If the input edges are not Delaunay,
the algorithm creates a constrained Delaunay triangulation.
(You don't have to prove this.)
running time.
If the input edges are not Delaunay,
the algorithm creates a constrained Delaunay triangulation.
(You don't have to prove this.)
[14] Nearest neighbors in curve reconstruction (4 points). Let S be a point set that 0.3-samples a curve F. Let x be a point in S, and let y be its nearest neighbor in S. Prove that x and y are adjacent samples on F, so the edge xy should be included in any reconstruction. (You should only need Amenta, Bern, and Eppstein's Lemma 1 to prove this.)
[15] Triangulate a PSLG in ![]() time (4 points).
In Lecture 1, we learned a method of regularizing simple polygons
(i.e., partitioning them into y-monotone polygons).
Generalize the algorithm so that it works for segment-bounded PSLGs.
(A PSLG is segment-bounded if the boundary between the
region we want to triangulate and the region we don't is a union of segments.)
You'll need to identify what types of vertices appear in PSLGs
but not in simple polygons,
and for each new vertex type either give pseudocode for handling it,
or explain why it can be handled exactly like some other vertex type.
time (4 points).
In Lecture 1, we learned a method of regularizing simple polygons
(i.e., partitioning them into y-monotone polygons).
Generalize the algorithm so that it works for segment-bounded PSLGs.
(A PSLG is segment-bounded if the boundary between the
region we want to triangulate and the region we don't is a union of segments.)
You'll need to identify what types of vertices appear in PSLGs
but not in simple polygons,
and for each new vertex type either give pseudocode for handling it,
or explain why it can be handled exactly like some other vertex type.