
We study the problem of moving packets around in a parallel computer. In this lecture we will consider parallel computers with hypercube connection networks. The methods we describe are easy to adapt to other connection networks, like butterflies or fat trees. An 8-processor machine is shown below.

The processors are at the vertices of the cube, and edges represent communication links. Each processor is numbered with a 3-bit binary number. Notice that the processor numbers are also X-Y-Z coordinates of the 3d layout of the cube.
A hypercube is a higher-dimensional cube. You can create a hypercube in N+1 dimensions from an N-dimensional by making an extra copy of the N-dimensional cube, and adding an extra bit which is zero in one copy and one in the other. Then join corresponding vertices. E.g. a 4D hypercube can be built from the 3D hypercube this way as shown below.

The processors are numbered with 4-bit binary numbers which represent the X-Y-Z-W coordinates (aside, this is a perfectly valid projection of 4D space, and this is exactly what the 4D cube looks like. Projecting from 4D or N-D into 2D is exactly analogous to 3D projection).
Processor number i wants to send a packet vi to destination d(i). We assume that the computer runs synchronously, so that all processors try to send their packets at the same time.
In permutation routing, every processor tries to send to a different destination. That is, the function d(i) is a permutation.
The route taken by a packet vi depends only on its destination d(i) and not on any other packet’s destination d(j).
Oblivious routing is the most practical method to use for parallel computers. Routing which is not oblivious requires central coordination. But that implies that some processor is able to look at the destinations of many packets in the current time step and compute a good global routing for them. This takes a considerable amount of time and communication. It is certainly not a good idea to use it for routing packets, which is the lowest level operation that the parallel machine performs. Routing must be very fast because all of the high level machine operations rely on it. E.g. some machines even borrow main memory from other machines on the network. So they must access that memory even faster than the simplest computations.
A collision occurs when two packets arrive at the same processor at the same time and try to leave via the same link.
Bit fixing is a simple process for routing a single packet obliviously. Take the bit address of the source processor and change one bit at a time to the address of the destination processor. Each time a bit is changed, the packet is forwarded to a neighboring processor.
This works because in a hypercube, each processor i is connected to all the processors j whose bit addresses differ from i in one bit. E.g. processor 1011 is connected to processor 0011, processor 1111, processor 1001 and processor 1010. So changing one bit of the address corresponds to sending the packet from the current node to a neighboring node.
It should be clear that bit fixing is an optimal routing scheme for a single packet. If the source i and destination address j differ by k bits, then the packet must traverse at least k links in the hypercube to get to its destination. Bit fixing gets it there in exactly k steps.
If we have to route many packets though, even if the routing is a permutation routing, bit fixing can cause collisions. In fact, so can any deterministic oblivious routing strategy. To deal with collisions, every processor has a queue and a prioritizing scheme for each incoming packet. If incoming packets try to leave along the same link, they are placed in a queue and sent off in different time steps.
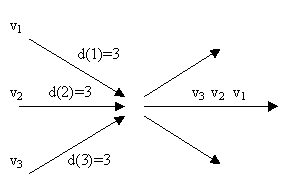
e.g. in the figure above, three packets arrive at the same node and attempt to leave along the same link (we show their destinations as the same which doesn’t happen with permutation routing, but what we really mean is that the next node address is the same). If the 3 packets arrive at time step T, the packets are queued, and v1 leaves in time step T+1, v2 leaves at T+2, and v3 leaves at T+3.
Thus routing can still occur with collisions, since all packets eventually get to their destinations, but there may be long delays because of queueing. In fact we have:
Any determistic oblivious permutation routing scheme for a parallel machine with N processors each with n outward links requires W (Ö (N/n)) steps.
Luckily we can avoid this bad case by using a randomized routing scheme. In fact most permutations cause very few collisions. So the idea is to first route all the packets using a random permutation, and then from there to their final destination. That is,
There is an important observation we can make about bit fixing. Namely, during a given phase of the above algorithm (step 1. or step 2.) two packets can come together along a route and then separate, but only once. That is, a pair of routes can look like the left picture but not the right:

To see this, notice that during bit fixing routing, an intermediate address always looks like
D1,…,Dk,Sk+1,…,Sn
where Si is a bit of the Source address, and Dj is a bit of the destination address. If two routes collide at the kth step, that means their destination addresses agree in their first k bits and the source addresses agree in their last n-k bits. Let k0 be the first value of k for which the packets collide. At each time step, we add one more bit of the destination address, which means we increment k. Eventually, the destination bits must disagree (because the destinations are different). Let k1 be the value of k at which this happens. Then the Dk1 destination bit is different for the two packets. At that point, the two packets separate. They will never collide again, because all the later intermediate destinations will include the Dk1 bit.
This observation is the crux of the proof of the following theorem:
The delay of a packet vi is £ |S| where S is the set of packets whose routes intersect vi’s route.
We won’t give a detailed proof. It’s enough to notice that whenever the routes of two packets intersect, one of the packets may be delayed by one time step. Once that packet is delayed by one time step at the first shared node, it will flow along the shared route behind the other packet, and will not be delayed any more by that packet.
If the same route intersects other routes, each of them may add a delay of one time step. This happens either (i) because another packet collides with the current packet along a shared route, or (ii) because another packet collides with a packet that is ahead of the current packet along a part of the route which is shared by all three. In either case, an extra delay of at most one results.
To get the running time of this scheme, we compute the expected value of the size of the set S above. Define an indicator random variable Hij which is 1 when the routes of packet vi and packet vj share at least one edge, and Hij is 0 otherwise. Then by the above theorem, the expected delay of packet vi is the expected size of S which is
![]()
It’s rather difficult to an exact estimate of this quantity because Hij is a complicated condition. It’s easier to think about T(e) which is the number of routes that pass through a given edge e. Now suppose the route of packet vi consists of the edges (e1, e2,…, ek). Then it turns out that:
![]()
This inequality can be proved by induction on the number of routes. Each time you add a new route, you increment the LHS by one for every route that the new route intersects. But you increment the RHS by k for each route that the new route intersects, where k is the number of edges that the two routes share.
And so
![]()
To use this bound we next compute E[T(e)] which turns out to be ½. To see that, notice that
E[T(e)] = (sum of lengths of all routes)/(total edges in the network)
The sum of lengths of all routes is the expected length of a route times N (the number of all routes). The average length of a route is n/2 because an n-bit source differs from a random destination address is n/2 bits on average. So the sum of route lengths is Nn/2.
The total number of edges in the network is the number of nodes times the number of outbound links, which is Nn. So
E[T(e)] = (Nn/2)/(Nn) = ½
Then if the path for packet vi has k edges along it, then
![]()
Now we can apply Chernoff bounds to the probability of there being a substantial number of paths intersecting vi’s path. The Chernoff bound is
![]()
Aside: This is the Chernoff bound for large d > 2e-1.
And so if (1+d)m = 6n, then since m =0.5n, d =11. Thus the probability is bounded by 2-5.5n.
This is a bound for the probability that a given packet is delayed more than 6n steps. But we would like to get a bound for the probability that no packet gets delayed more than 6n steps. For that, it’s enough to use the sum rule for probabilities as a bound. There are N = 2n routes total, and the probability that none of these takes more than 6n steps is bounded above by
2n 2-5.5n = 2-4.5n
So we can make the following assertion:
With probability at least 1 – 2-4.5n every packet reaches its destination s (i) in 7n or fewer steps.
The 7n comes from the delay time (6n) plus the time for the bit fixing steps, which is £ n. Notice that all of this applies to just one phase of the algorithm (recall that phase one routes a packet to a random location, and phase two routes from there to the actual destination). So the full algorithm routes all packets to their destinations with high probability in 14n or fewer steps.