On the Quality of a Semidefinite Programming Bound for Sparse Principal Component Analysis
Download: http://arxiv.org/abs/math/0601448.
Author: L. El Ghaoui.
Status: Preprint on arXiv.
Abstract: We examine the problem of approximating a positive, semidefinite matrix
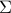 by a dyad
by a dyad 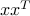 , with a penalty on the cardinality of the vector
, with a penalty on the cardinality of the vector 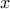 . This problem arises in sparse principal component analysis, where a decomposition of
. This problem arises in sparse principal component analysis, where a decomposition of 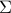 involving sparse factors is sought. We express this hard, combinatorial problem as a maximum eigenvalue problem, in which we seek to maximize, over a box, the largest eigenvalue of a symmetric matrix that is linear in the variables. This representation allows to use the techniques of robust optimization, to derive a bound based on semidefinite programming. The quality of the bound is investigated using a technique inspired by Nemirovski and Ben-Tal (2002).
involving sparse factors is sought. We express this hard, combinatorial problem as a maximum eigenvalue problem, in which we seek to maximize, over a box, the largest eigenvalue of a symmetric matrix that is linear in the variables. This representation allows to use the techniques of robust optimization, to derive a bound based on semidefinite programming. The quality of the bound is investigated using a technique inspired by Nemirovski and Ben-Tal (2002).
Related entries:
A. d'Aspremont, F. Bach, L. El Ghaoui. Optimal Solutions for Sparse Principal Component Analysis.
Bibtex reference:
@unpublished{Elg:06,
Author = {L. {El Ghaoui}},
Month = {February},
Note = {arXiv:math/060144},
Title = {On the Quality of a Semidefinite Programming
Bound for Sparse Principal Component Analysis},
Year = {2006}}