\input bkmacs
\photo{{\it Apple Tree in Blossom,\/} Piet Mondrian
(1912)}{\pagetag{\mondrian}\pspicture{4in}{mondrian}{mondrian}{\TrimBoundingBox{5pt}}}
\chapter{Trees}
\chaptag{\trees}
The big advantage of full-featured lists over sentences is their ability to
represent {\it structure\/} in our data by means of sublists.
In this chapter we'll look at examples in which we use lists and sublists to
represent two-dimensional information structures. The kinds of structures
we'll consider are called {\it \idx{tree}s\/} because they resemble trees in
nature:
\htstart
 \htend
% \pspicture{2in}{Computer Science Tree
% and Real Tree}{firsttree}{\rlap{\hskip
% 2truein\pspicture{1.5in}{tree}{tree}{}}\hSlide{-1.5truein}}
\noindent The components of a tree are called {\it \idx{node}s.\/} At the
top is the {\it \bkidx{root}{node}\/} of the tree; in the interior of the
diagram there are {\it \bkidx{branch}{node}s;\/} at the bottom are the {\it
\bkidx{leaf}{node}s,\/} from which no further branches extend.
We're going to begin by considering a tree as an abstract data type, without
thinking about how lists are used to represent trees. For example, we'll
construct trees using a procedure named {\tt make-node}, as if that were a
Scheme primitive. About halfway through the chapter, we'll explore the
relationship between trees and lists.
\goodbreak
\subhd{Example:\ The World}
Here is a tree that represents the world:
\pspicture{3in}{The World Tree}{world}{\TrimBoundingBox{10pt}}
Each node in the tree represents some region of the world. Consider the
node labeled ``Great Britain.'' There are two parts to this node: The
obvious part is the label itself, the name ``Great Britain.'' But
the regions of the world that are included within Great Britain---that is,
the nodes that are attached beneath Great Britain in the figure---are also part
of this node.
We say that every node has a {\it \idx{datum}\/} and zero or more {\it
\idx{children}.\/} For the moment, let's just say that the datum can be
either a word or a sentence. The children, if any, are themselves trees.
Notice that this definition is recursive---a tree is made up of trees.
(What's the base case?)
This family metaphor is also part of the terminology of
trees.\footnt{Contrariwise, the tree metaphor is also part of the
terminology of families.} We say that a node is the {\it \idx{parent}\/} of
another node, or that two nodes are {\it \idx{sibling}s.\/} In more advanced
treatments, you even hear things like ``grandparent'' and ``cousin,'' but we
won't get into that.
What happens when you prune an actual tree by cutting off a branch?
The cut-off part is essentially a tree in itself, with a smaller trunk
and fewer branches. The metaphor isn't perfect because the cut-off part
doesn't have roots, but still, we can stick the end in the ground and
hope that the cut-off end will take root as a new tree.
It's the same with a country in our example; each country is a branch node of
the entire world tree, but also a tree in itself. Depending on how you
think about it, Great Britain can be either a component of the entire world
or a collection of smaller locations. So the branch node that represents
Great Britain is the root node of a {\it \idx{subtree}\/} of the entire tree.
\pspicture{2in}{The Great Britain Subtree}{britain}{\TrimTop{0.35truein}}
What is a node? It might seem natural to think of a node as being just the
information in one of the circles in the diagram---that is, to think of a
node as including only its datum. In that way of thinking, each node would
be separate from every other node, just as the words in a sentence are all
separate elements. However, it will be more useful to think of a node as a
structure that includes everything below that circle also:\ the datum and the
children. So when we think of the node for Great Britain, we're thinking
not only of the name ``Great Britain,'' but also of everything {\it
in\/} Great Britain. From this perspective, the root node of a tree
includes the entire tree. We might as well say that the node {\it is\/} the
tree.
The \idx{constructor} for a tree is actually the constructor for one node,
its root node. Our constructor for trees is therefore called
{\tt \ttidx{make-node}}. It takes two arguments:\ the datum and a (possibly
empty) list of children. As the following example shows, constructing what
we think of as one tree requires the construction of many such nodes.
{\prgex%
(define world-tree ;; painful-to-type version
(make-node
'world
(list (make-node
'italy
(list (make-node 'venezia '())
(make-node 'riomaggiore '())
(make-node 'firenze '())
(make-node 'roma '())))
(make-node
'(united states)
(list (make-node 'california
(list (make-node 'berkeley '())
(make-node '(san francisco) '())
(make-node 'gilroy '())))
(make-node 'massachusetts
(list (make-node 'cambridge '())
(make-node 'amherst '())
(make-node 'sudbury '()))))))))
}
\noindent You'll notice that we haven't defined all of the places shown
in the figure. That's because we got tired of doing all this typing;
we're going to invent some abbreviations later. For now, we'll take time
out to show you the \idx{selector}s for trees.
\justtt{datum}
\justtt{children}
{\prgex%
> (datum world-tree)
WORLD
> (datum (car (children world-tree)))
ITALY
> (datum (car (children (cadr (children world-tree)))))
CALIFORNIA
> (datum (car (children (car (children
(cadr (children world-tree)))))))
BERKELEY
}
\noindent {\tt Datum} of a tree node returns the datum of that node.
{\tt Children} of a node returns a list of the children of the node.
(A list of trees is called a {\it \idx{forest}.\/})
Here are some abbreviations to help us construct the world tree with less
typing. Unlike {\tt make-node}, {\tt datum}, and {\tt children}, which are
intended to work on trees in general, these abbreviations were designed
with the world tree specifically in mind:
{\prgex%
(define (\ufun{leaf} datum)
(make-node datum '()))
(define (\ufun{cities} name-list)
(map leaf name-list))
}
\noindent With these abbreviations the world tree is somewhat easier to
define:
{\prgex%
(define world-tree
(make-node
'world
(list (make-node
'italy
(cities '(venezia riomaggiore firenze roma)))
(make-node
'(united states)
(list (make-node
'california
(cities '(berkeley (san francisco) gilroy)))
(make-node
'massachusetts
(cities '(cambridge amherst sudbury)))
(make-node 'ohio (cities '(kent)))))
(make-node 'zimbabwe (cities '(harare hwange)))
(make-node 'china
(cities '(beijing shanghai guangzhou suzhou)))
(make-node
'(great britain)
(list
(make-node 'england (cities '(liverpool)))
(make-node 'scotland
(cities '(edinburgh glasgow (gretna green))))
(make-node 'wales (cities '(abergavenny)))))
(make-node
'australia
(list
(make-node 'victoria (cities '(melbourne)))
(make-node '(new south wales) (cities '(sydney)))
(make-node 'queensland
(cities '(cairns (port douglas))))))
(make-node 'honduras (cities '(tegucigalpa))))))
}
\subhd{How Big Is My Tree?}
Now that we have the tree, how many cities are there in our world?
{\prgex%
(define (\ufun{count-leaves} tree)
(if (leaf? tree)
1
(reduce + (map count-leaves (children tree)))))
(define (\ufun{leaf?} node)
(null? (children node)))
> (count-leaves world-tree)
27
}
At first glance, this may seem like a simple case of recursion, with
{\tt count-leaves} calling {\tt count-leaves}. But since what looks like a
single recursive call is really a call to {\tt map}, it is equivalent to
{\it several\/} recursive calls, one for each child of the given tree node.
\backskipsubhd{Mutual Recursion}{4}
{\advance\medskipamount by -2pt
In Chapter \recpatt\ we wrote recursive
procedures that were equivalent to using higher-order functions. Let's do
the same for {\tt count-leaves}.
{\prgex%
(define (\ufun{count-leaves} tree)
(if (leaf? tree)
1
(count-leaves-in-forest (children tree))))
(define (\ufun{count-leaves-in-forest} forest)
(if (null? forest)
0
(+ (count-leaves (car forest))
(count-leaves-in-forest (cdr forest)))))
}
%%%%% kludge coming up %%%%%
\hyphenchar\tentt=\count123
\noindent Note that {\tt count-leaves} calls {\tt count-leaves-in-forest},
and {\tt count-leaves-}\penalty-200{\tt in-}\penalty-200{\tt forest} calls
{\tt count-leaves}. This pattern is called {\it \bkidx{mutual}{recursion}.}
\hyphenchar\tentt=-1
Mutual recursion is often a useful technique for dealing with trees. In the
typical recursion we've seen before this chapter, we've moved sequentially
through a list or sentence, with each recursive call taking us one step to
the right. In the following paragraphs we present three different models to
help you think about how the shape of a tree gives rise to a mutual recursion.
In the first model, we're going to think of {\tt count-leaves} as an
initialization procedure, and {\tt count-leaves-in-forest} as its helper
procedure. Suppose we want to count the leaves of a tree. Unless the
argument is a very shallow\footnt{You probably think of trees as being short
or tall. But since our trees are upside-down, the convention is to call
them shallow or deep.} tree, this will involve counting the leaves of all
of the children of that tree. What we want is a straightforward sequential
recursion over the list of children. But we're given the wrong argument:\
the tree itself, not its list of children. So we need an initialization
procedure, {\tt count-leaves}, whose job is to extract the list of children
and invoke a helper procedure, {\tt count-leaves-in-forest}, with that list
as argument.
The helper procedure follows the usual sequential list pattern: Do
something to the {\tt car} of the list, and recursively handle the {\tt cdr}
of the list. Now, what do we have to do to the {\tt car}? In the usual
sequential recursion, the {\tt car} of the list is something simple, such as
a word. What's special about trees is that here the {\tt car} is itself a
tree, just like the entire data structure we started with. Therefore, we
must invoke a procedure whose domain is trees:\ {\tt count-leaves}.
This model is built on two ideas. One is the idea of the domain of a
function; the reason we need two procedures is that we need one that takes a
tree as its argument and one that takes a list of trees as its argument.
The other idea is the leap of faith; we assume that the invocation of {\tt
count-leaves} within {\tt count-leaves-in-forest} will correctly handle each
child without tracing the exact sequence of events.
The second model is easier to state but less rigorous. Because of the
two-dimensional nature of trees, in order to visit every node we have to be
able to move in two different directions. From a given node we have to be
able to move {\it down\/} to its children, but from each child we must be
able to move {\it across\/} to its next sibling.
The job of {\tt count-leaves-in-forest} is to move from left to right
through a list of children. (It does this using the more familiar kind of
recursion, in which it invokes itself directly.) The downward motion
happens in {\tt count-leaves}, which moves down one level by invoking {\tt
children}. How does the program move down more than one level? At each
level, {\tt count-leaves} is invoked recursively from {\tt
count-leaves-in-forest}.
The third model is also based on the two-dimensional nature of trees.
Imagine for a moment that each node in the tree has at most one child.
In that case, {\tt count-leaves} could move from the root down to the single
leaf with a structure very similar to the actual procedure, but carrying out
a sequential recursion:
{\prgex%
(define (count-leaf tree)
(if (leaf? tree)
1
(count-leaf (child tree))))
}
\noindent The trouble with this, of course, is that at each downward
step there isn't a single ``next'' node. Instead of a single path from the
root to the leaf, there are multiple paths from the root to many leaves.
To make our idea of downward motion through sequential recursion work in a
real tree, at each level we must ``clone'' {\tt count-leaves} as many times
as there are children. {\tt Count-leaves-in-forest} is the factory that
manufactures the clones. It hires one {\tt count-leaves} little person for
each child and accumulates their results.
The key point in recursion on trees is that each child of a tree is itself a
perfectly good tree. This recursiveness in the nature of trees gives rise
to a very recursive structure for programs that use trees. The reason we
say ``very'' recursive is that each invocation of {\tt count-leaves} causes
not just one but several recursive invocations, one for each child, by way
of {\tt count-leaves-in-forest}.
In fact, we use the name {\it \bkidx{tree}{recursion}\/} for any situation
in which a procedure invocation results in more than one recursive call,
even if there isn't an argument that's a tree. The computation of Fibonacci
numbers from Chapter \convince\ is an example of a tree recursion with no
tree. The {\tt car}-{\tt cdr} recursions in Chapter~\lists\ are also
tree recursions; any structured list-of-lists has a somewhat tree-like,
two-dimensional character even though it doesn't use the formal mechanisms
we're exploring in this chapter.
The {\tt cdr} recursion is a ``horizontal'' one, moving from one element
to another within the same list; the {\tt car} recursion is a ``vertical''
one, exploring a sublist of the given list.
\backskipsubhd{Searching for a Datum in the Tree}{5}
Procedures that explore trees aren't always as simple as {\tt count-leaves}.
We started with that example because we could write it using higher-order
functions, so that you'd understand the structure of the problem before we
had to take on the complexity of mutual recursion. But many tree problems
don't quite fit our higher-order functions.
For example, let's write a predicate {\tt in-tree?}\ that takes the name of
a place and a tree as arguments and tells whether or not that place is in the
tree. It {\it is\/} possible to make it work with {\tt filter}:
{\prgex%
(define (\ufun{in-tree?} place tree)
(or (equal? place (datum tree))
(not (null? (filter (lambda (subtree) (in-tree? place subtree))
(children tree))))))
}
\noindent This awkward construction, however, also performs
unnecessary computation. If the place we're looking for happens to be in the
first child of a node, {\tt filter} will nevertheless look in all the other
children as well. We can do better by replacing the use of {\tt filter}
with a mutual recursion:
{\prgex%
(define (\ufun{in-tree?} place tree)
(or (equal? place (datum tree))
(in-forest? place (children tree))))
(define (\ufun{in-forest?} place forest)
(if (null? forest)
#f
(or (in-tree? place (car forest))
(in-forest? place (cdr forest)))))
> (in-tree? 'abergavenny world-tree)
\#T
> (in-tree? 'abbenay world-tree)
\#F
> (in-tree? 'venezia (cadr (children world-tree)))
\#F
}
Although any mutual recursion is a little tricky to read, the structure
of this program does fit the way we'd describe the algorithm in
English. A place is in a tree if one of two conditions holds:\ the place is
the datum at the root of the tree, or the place is (recursively) in one of
the child trees of this tree. That's what {\tt in-tree?}\ says. As for
{\tt in-forest?}, it says that a place is in one of a group of trees if
the place is in the first tree, or if it's in one of the remaining trees.
\subhd{Locating a Datum in the Tree}
Our next project is similar to the previous one, but a little more
intricate. We'd like to be able to locate a city and find out all of
the larger regions that enclose the city. For example, we want to say
{\prgex%
> (locate 'berkeley world-tree)
(WORLD (UNITED STATES) CALIFORNIA BERKELEY)
}
\noindent Instead of just getting a yes-or-no answer about whether a city is
in the tree, we now want to find out {\it where\/} it is.
The algorithm is recursive: To look for Berkeley within the world, we need
to be able to look for Berkeley within any subtree. The {\tt world} node
has several children (countries). {\tt Locate} recursively asks each of
those children to find a path to Berkeley. All but one of the children
return {\tt #f}, because they can't find Berkeley within their territory.
But the {\tt (united~states)} node returns
{\prgex%
((UNITED STATES) CALIFORNIA BERKELEY)
}
\noindent To make a complete path, we just prepend the name of the current
node, {\tt world}, to this path. What happens when {\tt locate} tries to
look for Berkeley in Australia? Since all of Australia's children return
{\tt #f}, there is no path to Berkeley from Australia, so {\tt locate}
returns {\tt #f}.
{\prgex%
(define (\ufun{locate} city tree)
(if (equal? city (datum tree))
(list city)
(let ((subpath (locate-in-forest city (children tree))))
(if subpath
(cons (datum tree) subpath)
\#f))))
(define (\ufun{locate-in-forest} city forest)
(if (null? forest)
#f
(or (locate city (car forest))
(locate-in-forest city (cdr forest)))))
}
Compare the structure of {\tt locate} with that of {\tt in-tree?}. The
helper procedures {\tt in-forest?}\ and {\tt locate-in-forest} are almost
identical. The main procedures look different, because {\tt locate} has a
harder job, but both of them check for two possibilities: The city might be
the datum of the argument node, or it might belong to one of the child trees.
\subhd{Representing Trees as Lists}
We've done a lot with trees, but we haven't yet talked about the way Scheme
stores trees internally. How do {\tt make-node}, {\tt datum}, and {\tt
children} work? It turns out to be very convenient to represent trees in
terms of lists.
{\prgex%
(define (\ufun{make-node} datum children)
(cons datum children))
(define (\ufun{datum} node)
(car node))
(define (\ufun{children} node)
(cdr node))
}
\noindent In other words, a tree is a list whose first element is the datum
and whose remaining elements are subtrees.
\kludgect
{\prgex%
> world-tree
(WORLD
(ITALY (VENEZIA) (RIOMAGGIORE) (FIRENZE) (ROMA))
((UNITED STATES)
(CALIFORNIA (BERKELEY) ((SAN FRANCISCO)) (GILROY))
(MASSACHUSETTS (CAMBRIDGE) (AMHERST) (SUDBURY))
(OHIO (KENT)))
(ZIMBABWE (HARARE) (HWANGE))
(CHINA (BEIJING) (SHANGHAI) (GUANGSZHOU) (SUZHOW))
((GREAT BRITAIN)
(ENGLAND (LIVERPOOL))
(SCOTLAND (EDINBURGH) (GLASGOW) ((GRETNA GREEN)))
(WALES (ABERGAVENNY)))
(AUSTRALIA
(VICTORIA (MELBOURNE))
((NEW SOUTH WALES) (SYDNEY))
(QUEENSLAND (CAIRNS) ((PORT DOUGLAS))))
(HONDURAS (TEGUCIGALPA)))
}
{\prgex%
> (car (children world-tree))
(ITALY (VENEZIA) (RIOMAGGIORE) (FIRENZE) (ROMA))
}
Ordinarily, however, we're not going to print out trees in their entirety.
As in the {\tt locate} example, we'll extract just some subset of the
information and put it in a more readable form.
\subhd{Abstract Data Types}
The procedures {\tt make-node}, {\tt datum}, and {\tt children} define an
\bkidx{abstract}{data type} for trees. Using this ADT,
\justidx{type, abstract}
\justidx{ADT}
we were able to write several useful procedures to manipulate trees before
pinning down exactly how a tree is represented as a Scheme list.
Although it would be possible to refer to the parts of a node by using {\tt
car} and {\tt cdr} directly, your programs will be more readable if you use
the ADT-specific selectors and constructors. Consider this example:
{\prgex%
(in-tree? 'venezia (caddr world-tree))
}
\noindent What does {\tt caddr} mean in this context? Is the {\tt caddr} of
a tree a datum? A child? A forest? Of course you could work it out by
careful reasoning, but the form in which we presented this example
originally was much clearer:
{\prgex%
(in-tree? 'venezia (cadr (children world-tree)))
}
\noindent Even better would be
{\prgex%
(in-tree? 'venezia (list-ref (children world-tree) 1))
}
Using the appropriate selectors and constructors is called {\it
respecting\/} the data abstraction. Failing to use the appropriate
selectors and constructors is called a {\it \idx{data abstraction
violation}.\/}
Since we wrote the selectors and constructor for trees ourselves, we
could have defined them to use some different representation:
{\prgex%
(define (make-node datum children)
(list 'the 'node 'with 'datum datum 'and 'children children))
(define (datum node) (list-ref node 4))
(define (children node) (list-ref node 7))
}
{\prgex%
> (make-node 'italy (cities '(venezia riomaggiore firenze roma)))
(THE NODE WITH DATUM ITALY AND CHILDREN
((THE NODE WITH DATUM VENEZIA AND CHILDREN ())
(THE NODE WITH DATUM RIOMAGGIORE AND CHILDREN ())
(THE NODE WITH DATUM FIRENZE AND CHILDREN ())
(THE NODE WITH DATUM ROMA AND CHILDREN ())))
}
\noindent You might expect that this change in the representation would
require changes to all the procedures we wrote earlier, such as {\tt
count-leaves}. But in fact, those procedures would continue to work
perfectly because they don't see the representation. (They respect the data
abstraction.) As long as {\tt datum} and {\tt children} find the right
information, it doesn't matter how the trees are stored. All that matters
is that the constructors and selectors have to be compatible with each other.
On the other hand, the example in this section in which we violated the data
abstraction by using {\tt caddr} to find the second child of {\tt
world-tree} would fail if we changed the representation. Many cases like
this one, in which formerly working programs failed after a change in
representation, led programmers to use such moralistic terms as
``respecting'' and ``violating'' data abstractions.\footnt{Another example
of a data abstraction violation is in Chapter \match. When {\tt match} creates
an empty known-values database, we didn't use a constructor. Instead, we
merely used a quoted empty sentence:
{\prgex%
(define (match pattern sent)
(match-using-known-values pattern sent '()))
}}
} % medskipamount
\subhd{An Advanced Example: Parsing Arithmetic Expressions}
Consider the notation for arithmetic expressions. Scheme uses {\it
\justidx{prefix notation}
\justidx{infix notation}
prefix\/} notation:\ {\tt (+~3~4)}. By contrast, people who aren't Scheme
programmers generally represent arithmetic computations using an {\it
infix\/} notation, in which the function symbol goes between two
arguments:\ $3+4$.
Our goal in this section is to translate an infix arithmetic expression into
a tree representing the computation. This translation process is called
{\it parsing\/} the expression. For example, we'll turn the expression
\htstart
4+3×7-5/(3+4)+6
\htend
% \pspicture{2in}{Computer Science Tree
% and Real Tree}{firsttree}{\rlap{\hskip
% 2truein\pspicture{1.5in}{tree}{tree}{}}\hSlide{-1.5truein}}
\noindent The components of a tree are called {\it \idx{node}s.\/} At the
top is the {\it \bkidx{root}{node}\/} of the tree; in the interior of the
diagram there are {\it \bkidx{branch}{node}s;\/} at the bottom are the {\it
\bkidx{leaf}{node}s,\/} from which no further branches extend.
We're going to begin by considering a tree as an abstract data type, without
thinking about how lists are used to represent trees. For example, we'll
construct trees using a procedure named {\tt make-node}, as if that were a
Scheme primitive. About halfway through the chapter, we'll explore the
relationship between trees and lists.
\goodbreak
\subhd{Example:\ The World}
Here is a tree that represents the world:
\pspicture{3in}{The World Tree}{world}{\TrimBoundingBox{10pt}}
Each node in the tree represents some region of the world. Consider the
node labeled ``Great Britain.'' There are two parts to this node: The
obvious part is the label itself, the name ``Great Britain.'' But
the regions of the world that are included within Great Britain---that is,
the nodes that are attached beneath Great Britain in the figure---are also part
of this node.
We say that every node has a {\it \idx{datum}\/} and zero or more {\it
\idx{children}.\/} For the moment, let's just say that the datum can be
either a word or a sentence. The children, if any, are themselves trees.
Notice that this definition is recursive---a tree is made up of trees.
(What's the base case?)
This family metaphor is also part of the terminology of
trees.\footnt{Contrariwise, the tree metaphor is also part of the
terminology of families.} We say that a node is the {\it \idx{parent}\/} of
another node, or that two nodes are {\it \idx{sibling}s.\/} In more advanced
treatments, you even hear things like ``grandparent'' and ``cousin,'' but we
won't get into that.
What happens when you prune an actual tree by cutting off a branch?
The cut-off part is essentially a tree in itself, with a smaller trunk
and fewer branches. The metaphor isn't perfect because the cut-off part
doesn't have roots, but still, we can stick the end in the ground and
hope that the cut-off end will take root as a new tree.
It's the same with a country in our example; each country is a branch node of
the entire world tree, but also a tree in itself. Depending on how you
think about it, Great Britain can be either a component of the entire world
or a collection of smaller locations. So the branch node that represents
Great Britain is the root node of a {\it \idx{subtree}\/} of the entire tree.
\pspicture{2in}{The Great Britain Subtree}{britain}{\TrimTop{0.35truein}}
What is a node? It might seem natural to think of a node as being just the
information in one of the circles in the diagram---that is, to think of a
node as including only its datum. In that way of thinking, each node would
be separate from every other node, just as the words in a sentence are all
separate elements. However, it will be more useful to think of a node as a
structure that includes everything below that circle also:\ the datum and the
children. So when we think of the node for Great Britain, we're thinking
not only of the name ``Great Britain,'' but also of everything {\it
in\/} Great Britain. From this perspective, the root node of a tree
includes the entire tree. We might as well say that the node {\it is\/} the
tree.
The \idx{constructor} for a tree is actually the constructor for one node,
its root node. Our constructor for trees is therefore called
{\tt \ttidx{make-node}}. It takes two arguments:\ the datum and a (possibly
empty) list of children. As the following example shows, constructing what
we think of as one tree requires the construction of many such nodes.
{\prgex%
(define world-tree ;; painful-to-type version
(make-node
'world
(list (make-node
'italy
(list (make-node 'venezia '())
(make-node 'riomaggiore '())
(make-node 'firenze '())
(make-node 'roma '())))
(make-node
'(united states)
(list (make-node 'california
(list (make-node 'berkeley '())
(make-node '(san francisco) '())
(make-node 'gilroy '())))
(make-node 'massachusetts
(list (make-node 'cambridge '())
(make-node 'amherst '())
(make-node 'sudbury '()))))))))
}
\noindent You'll notice that we haven't defined all of the places shown
in the figure. That's because we got tired of doing all this typing;
we're going to invent some abbreviations later. For now, we'll take time
out to show you the \idx{selector}s for trees.
\justtt{datum}
\justtt{children}
{\prgex%
> (datum world-tree)
WORLD
> (datum (car (children world-tree)))
ITALY
> (datum (car (children (cadr (children world-tree)))))
CALIFORNIA
> (datum (car (children (car (children
(cadr (children world-tree)))))))
BERKELEY
}
\noindent {\tt Datum} of a tree node returns the datum of that node.
{\tt Children} of a node returns a list of the children of the node.
(A list of trees is called a {\it \idx{forest}.\/})
Here are some abbreviations to help us construct the world tree with less
typing. Unlike {\tt make-node}, {\tt datum}, and {\tt children}, which are
intended to work on trees in general, these abbreviations were designed
with the world tree specifically in mind:
{\prgex%
(define (\ufun{leaf} datum)
(make-node datum '()))
(define (\ufun{cities} name-list)
(map leaf name-list))
}
\noindent With these abbreviations the world tree is somewhat easier to
define:
{\prgex%
(define world-tree
(make-node
'world
(list (make-node
'italy
(cities '(venezia riomaggiore firenze roma)))
(make-node
'(united states)
(list (make-node
'california
(cities '(berkeley (san francisco) gilroy)))
(make-node
'massachusetts
(cities '(cambridge amherst sudbury)))
(make-node 'ohio (cities '(kent)))))
(make-node 'zimbabwe (cities '(harare hwange)))
(make-node 'china
(cities '(beijing shanghai guangzhou suzhou)))
(make-node
'(great britain)
(list
(make-node 'england (cities '(liverpool)))
(make-node 'scotland
(cities '(edinburgh glasgow (gretna green))))
(make-node 'wales (cities '(abergavenny)))))
(make-node
'australia
(list
(make-node 'victoria (cities '(melbourne)))
(make-node '(new south wales) (cities '(sydney)))
(make-node 'queensland
(cities '(cairns (port douglas))))))
(make-node 'honduras (cities '(tegucigalpa))))))
}
\subhd{How Big Is My Tree?}
Now that we have the tree, how many cities are there in our world?
{\prgex%
(define (\ufun{count-leaves} tree)
(if (leaf? tree)
1
(reduce + (map count-leaves (children tree)))))
(define (\ufun{leaf?} node)
(null? (children node)))
> (count-leaves world-tree)
27
}
At first glance, this may seem like a simple case of recursion, with
{\tt count-leaves} calling {\tt count-leaves}. But since what looks like a
single recursive call is really a call to {\tt map}, it is equivalent to
{\it several\/} recursive calls, one for each child of the given tree node.
\backskipsubhd{Mutual Recursion}{4}
{\advance\medskipamount by -2pt
In Chapter \recpatt\ we wrote recursive
procedures that were equivalent to using higher-order functions. Let's do
the same for {\tt count-leaves}.
{\prgex%
(define (\ufun{count-leaves} tree)
(if (leaf? tree)
1
(count-leaves-in-forest (children tree))))
(define (\ufun{count-leaves-in-forest} forest)
(if (null? forest)
0
(+ (count-leaves (car forest))
(count-leaves-in-forest (cdr forest)))))
}
%%%%% kludge coming up %%%%%
\hyphenchar\tentt=\count123
\noindent Note that {\tt count-leaves} calls {\tt count-leaves-in-forest},
and {\tt count-leaves-}\penalty-200{\tt in-}\penalty-200{\tt forest} calls
{\tt count-leaves}. This pattern is called {\it \bkidx{mutual}{recursion}.}
\hyphenchar\tentt=-1
Mutual recursion is often a useful technique for dealing with trees. In the
typical recursion we've seen before this chapter, we've moved sequentially
through a list or sentence, with each recursive call taking us one step to
the right. In the following paragraphs we present three different models to
help you think about how the shape of a tree gives rise to a mutual recursion.
In the first model, we're going to think of {\tt count-leaves} as an
initialization procedure, and {\tt count-leaves-in-forest} as its helper
procedure. Suppose we want to count the leaves of a tree. Unless the
argument is a very shallow\footnt{You probably think of trees as being short
or tall. But since our trees are upside-down, the convention is to call
them shallow or deep.} tree, this will involve counting the leaves of all
of the children of that tree. What we want is a straightforward sequential
recursion over the list of children. But we're given the wrong argument:\
the tree itself, not its list of children. So we need an initialization
procedure, {\tt count-leaves}, whose job is to extract the list of children
and invoke a helper procedure, {\tt count-leaves-in-forest}, with that list
as argument.
The helper procedure follows the usual sequential list pattern: Do
something to the {\tt car} of the list, and recursively handle the {\tt cdr}
of the list. Now, what do we have to do to the {\tt car}? In the usual
sequential recursion, the {\tt car} of the list is something simple, such as
a word. What's special about trees is that here the {\tt car} is itself a
tree, just like the entire data structure we started with. Therefore, we
must invoke a procedure whose domain is trees:\ {\tt count-leaves}.
This model is built on two ideas. One is the idea of the domain of a
function; the reason we need two procedures is that we need one that takes a
tree as its argument and one that takes a list of trees as its argument.
The other idea is the leap of faith; we assume that the invocation of {\tt
count-leaves} within {\tt count-leaves-in-forest} will correctly handle each
child without tracing the exact sequence of events.
The second model is easier to state but less rigorous. Because of the
two-dimensional nature of trees, in order to visit every node we have to be
able to move in two different directions. From a given node we have to be
able to move {\it down\/} to its children, but from each child we must be
able to move {\it across\/} to its next sibling.
The job of {\tt count-leaves-in-forest} is to move from left to right
through a list of children. (It does this using the more familiar kind of
recursion, in which it invokes itself directly.) The downward motion
happens in {\tt count-leaves}, which moves down one level by invoking {\tt
children}. How does the program move down more than one level? At each
level, {\tt count-leaves} is invoked recursively from {\tt
count-leaves-in-forest}.
The third model is also based on the two-dimensional nature of trees.
Imagine for a moment that each node in the tree has at most one child.
In that case, {\tt count-leaves} could move from the root down to the single
leaf with a structure very similar to the actual procedure, but carrying out
a sequential recursion:
{\prgex%
(define (count-leaf tree)
(if (leaf? tree)
1
(count-leaf (child tree))))
}
\noindent The trouble with this, of course, is that at each downward
step there isn't a single ``next'' node. Instead of a single path from the
root to the leaf, there are multiple paths from the root to many leaves.
To make our idea of downward motion through sequential recursion work in a
real tree, at each level we must ``clone'' {\tt count-leaves} as many times
as there are children. {\tt Count-leaves-in-forest} is the factory that
manufactures the clones. It hires one {\tt count-leaves} little person for
each child and accumulates their results.
The key point in recursion on trees is that each child of a tree is itself a
perfectly good tree. This recursiveness in the nature of trees gives rise
to a very recursive structure for programs that use trees. The reason we
say ``very'' recursive is that each invocation of {\tt count-leaves} causes
not just one but several recursive invocations, one for each child, by way
of {\tt count-leaves-in-forest}.
In fact, we use the name {\it \bkidx{tree}{recursion}\/} for any situation
in which a procedure invocation results in more than one recursive call,
even if there isn't an argument that's a tree. The computation of Fibonacci
numbers from Chapter \convince\ is an example of a tree recursion with no
tree. The {\tt car}-{\tt cdr} recursions in Chapter~\lists\ are also
tree recursions; any structured list-of-lists has a somewhat tree-like,
two-dimensional character even though it doesn't use the formal mechanisms
we're exploring in this chapter.
The {\tt cdr} recursion is a ``horizontal'' one, moving from one element
to another within the same list; the {\tt car} recursion is a ``vertical''
one, exploring a sublist of the given list.
\backskipsubhd{Searching for a Datum in the Tree}{5}
Procedures that explore trees aren't always as simple as {\tt count-leaves}.
We started with that example because we could write it using higher-order
functions, so that you'd understand the structure of the problem before we
had to take on the complexity of mutual recursion. But many tree problems
don't quite fit our higher-order functions.
For example, let's write a predicate {\tt in-tree?}\ that takes the name of
a place and a tree as arguments and tells whether or not that place is in the
tree. It {\it is\/} possible to make it work with {\tt filter}:
{\prgex%
(define (\ufun{in-tree?} place tree)
(or (equal? place (datum tree))
(not (null? (filter (lambda (subtree) (in-tree? place subtree))
(children tree))))))
}
\noindent This awkward construction, however, also performs
unnecessary computation. If the place we're looking for happens to be in the
first child of a node, {\tt filter} will nevertheless look in all the other
children as well. We can do better by replacing the use of {\tt filter}
with a mutual recursion:
{\prgex%
(define (\ufun{in-tree?} place tree)
(or (equal? place (datum tree))
(in-forest? place (children tree))))
(define (\ufun{in-forest?} place forest)
(if (null? forest)
#f
(or (in-tree? place (car forest))
(in-forest? place (cdr forest)))))
> (in-tree? 'abergavenny world-tree)
\#T
> (in-tree? 'abbenay world-tree)
\#F
> (in-tree? 'venezia (cadr (children world-tree)))
\#F
}
Although any mutual recursion is a little tricky to read, the structure
of this program does fit the way we'd describe the algorithm in
English. A place is in a tree if one of two conditions holds:\ the place is
the datum at the root of the tree, or the place is (recursively) in one of
the child trees of this tree. That's what {\tt in-tree?}\ says. As for
{\tt in-forest?}, it says that a place is in one of a group of trees if
the place is in the first tree, or if it's in one of the remaining trees.
\subhd{Locating a Datum in the Tree}
Our next project is similar to the previous one, but a little more
intricate. We'd like to be able to locate a city and find out all of
the larger regions that enclose the city. For example, we want to say
{\prgex%
> (locate 'berkeley world-tree)
(WORLD (UNITED STATES) CALIFORNIA BERKELEY)
}
\noindent Instead of just getting a yes-or-no answer about whether a city is
in the tree, we now want to find out {\it where\/} it is.
The algorithm is recursive: To look for Berkeley within the world, we need
to be able to look for Berkeley within any subtree. The {\tt world} node
has several children (countries). {\tt Locate} recursively asks each of
those children to find a path to Berkeley. All but one of the children
return {\tt #f}, because they can't find Berkeley within their territory.
But the {\tt (united~states)} node returns
{\prgex%
((UNITED STATES) CALIFORNIA BERKELEY)
}
\noindent To make a complete path, we just prepend the name of the current
node, {\tt world}, to this path. What happens when {\tt locate} tries to
look for Berkeley in Australia? Since all of Australia's children return
{\tt #f}, there is no path to Berkeley from Australia, so {\tt locate}
returns {\tt #f}.
{\prgex%
(define (\ufun{locate} city tree)
(if (equal? city (datum tree))
(list city)
(let ((subpath (locate-in-forest city (children tree))))
(if subpath
(cons (datum tree) subpath)
\#f))))
(define (\ufun{locate-in-forest} city forest)
(if (null? forest)
#f
(or (locate city (car forest))
(locate-in-forest city (cdr forest)))))
}
Compare the structure of {\tt locate} with that of {\tt in-tree?}. The
helper procedures {\tt in-forest?}\ and {\tt locate-in-forest} are almost
identical. The main procedures look different, because {\tt locate} has a
harder job, but both of them check for two possibilities: The city might be
the datum of the argument node, or it might belong to one of the child trees.
\subhd{Representing Trees as Lists}
We've done a lot with trees, but we haven't yet talked about the way Scheme
stores trees internally. How do {\tt make-node}, {\tt datum}, and {\tt
children} work? It turns out to be very convenient to represent trees in
terms of lists.
{\prgex%
(define (\ufun{make-node} datum children)
(cons datum children))
(define (\ufun{datum} node)
(car node))
(define (\ufun{children} node)
(cdr node))
}
\noindent In other words, a tree is a list whose first element is the datum
and whose remaining elements are subtrees.
\kludgect
{\prgex%
> world-tree
(WORLD
(ITALY (VENEZIA) (RIOMAGGIORE) (FIRENZE) (ROMA))
((UNITED STATES)
(CALIFORNIA (BERKELEY) ((SAN FRANCISCO)) (GILROY))
(MASSACHUSETTS (CAMBRIDGE) (AMHERST) (SUDBURY))
(OHIO (KENT)))
(ZIMBABWE (HARARE) (HWANGE))
(CHINA (BEIJING) (SHANGHAI) (GUANGSZHOU) (SUZHOW))
((GREAT BRITAIN)
(ENGLAND (LIVERPOOL))
(SCOTLAND (EDINBURGH) (GLASGOW) ((GRETNA GREEN)))
(WALES (ABERGAVENNY)))
(AUSTRALIA
(VICTORIA (MELBOURNE))
((NEW SOUTH WALES) (SYDNEY))
(QUEENSLAND (CAIRNS) ((PORT DOUGLAS))))
(HONDURAS (TEGUCIGALPA)))
}
{\prgex%
> (car (children world-tree))
(ITALY (VENEZIA) (RIOMAGGIORE) (FIRENZE) (ROMA))
}
Ordinarily, however, we're not going to print out trees in their entirety.
As in the {\tt locate} example, we'll extract just some subset of the
information and put it in a more readable form.
\subhd{Abstract Data Types}
The procedures {\tt make-node}, {\tt datum}, and {\tt children} define an
\bkidx{abstract}{data type} for trees. Using this ADT,
\justidx{type, abstract}
\justidx{ADT}
we were able to write several useful procedures to manipulate trees before
pinning down exactly how a tree is represented as a Scheme list.
Although it would be possible to refer to the parts of a node by using {\tt
car} and {\tt cdr} directly, your programs will be more readable if you use
the ADT-specific selectors and constructors. Consider this example:
{\prgex%
(in-tree? 'venezia (caddr world-tree))
}
\noindent What does {\tt caddr} mean in this context? Is the {\tt caddr} of
a tree a datum? A child? A forest? Of course you could work it out by
careful reasoning, but the form in which we presented this example
originally was much clearer:
{\prgex%
(in-tree? 'venezia (cadr (children world-tree)))
}
\noindent Even better would be
{\prgex%
(in-tree? 'venezia (list-ref (children world-tree) 1))
}
Using the appropriate selectors and constructors is called {\it
respecting\/} the data abstraction. Failing to use the appropriate
selectors and constructors is called a {\it \idx{data abstraction
violation}.\/}
Since we wrote the selectors and constructor for trees ourselves, we
could have defined them to use some different representation:
{\prgex%
(define (make-node datum children)
(list 'the 'node 'with 'datum datum 'and 'children children))
(define (datum node) (list-ref node 4))
(define (children node) (list-ref node 7))
}
{\prgex%
> (make-node 'italy (cities '(venezia riomaggiore firenze roma)))
(THE NODE WITH DATUM ITALY AND CHILDREN
((THE NODE WITH DATUM VENEZIA AND CHILDREN ())
(THE NODE WITH DATUM RIOMAGGIORE AND CHILDREN ())
(THE NODE WITH DATUM FIRENZE AND CHILDREN ())
(THE NODE WITH DATUM ROMA AND CHILDREN ())))
}
\noindent You might expect that this change in the representation would
require changes to all the procedures we wrote earlier, such as {\tt
count-leaves}. But in fact, those procedures would continue to work
perfectly because they don't see the representation. (They respect the data
abstraction.) As long as {\tt datum} and {\tt children} find the right
information, it doesn't matter how the trees are stored. All that matters
is that the constructors and selectors have to be compatible with each other.
On the other hand, the example in this section in which we violated the data
abstraction by using {\tt caddr} to find the second child of {\tt
world-tree} would fail if we changed the representation. Many cases like
this one, in which formerly working programs failed after a change in
representation, led programmers to use such moralistic terms as
``respecting'' and ``violating'' data abstractions.\footnt{Another example
of a data abstraction violation is in Chapter \match. When {\tt match} creates
an empty known-values database, we didn't use a constructor. Instead, we
merely used a quoted empty sentence:
{\prgex%
(define (match pattern sent)
(match-using-known-values pattern sent '()))
}}
} % medskipamount
\subhd{An Advanced Example: Parsing Arithmetic Expressions}
Consider the notation for arithmetic expressions. Scheme uses {\it
\justidx{prefix notation}
\justidx{infix notation}
prefix\/} notation:\ {\tt (+~3~4)}. By contrast, people who aren't Scheme
programmers generally represent arithmetic computations using an {\it
infix\/} notation, in which the function symbol goes between two
arguments:\ $3+4$.
Our goal in this section is to translate an infix arithmetic expression into
a tree representing the computation. This translation process is called
{\it parsing\/} the expression. For example, we'll turn the expression
\htstart
4+3×7-5/(3+4)+6
\htend
% $$4+3 \times 7-5/(3+4)+6$$
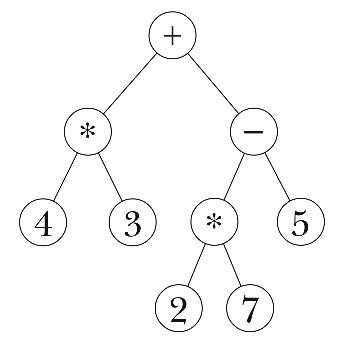
\noindent into the tree
\pspicture{1.5in}{Arithmetic expression tree}{parse0}{}
The point of using a tree is that it's going to be very easy to perform the
computation once we have it in tree form. In the original infix form, it's
hard to know what to do first, because there are {\it precedence\/} rules
that determine an implicit grouping: Multiplication and division come
before addition and subtraction; operations with the same precedence are
done from left to right. Our sample expression is equivalent to
\htstart
(((4 + (3 × 7)) - (5 / (3+4))) + 6)
\htend
% $$(((4 + (3 \times 7)) - (5 / (3+4))) + 6)$$
\noindent In the tree representation, it's easy to see that the operations
nearer the leaves are done first; the root node is the last operation,
because it depends on the results of lower-level operations.
Our program will take as its argument an infix arithmetic expression in the
form of a list:
{\prgex%
> (parse '(4 + 3 * 7 - 5 / (3 + 4) + 6))
}
\noindent Each element of the list must be one of three things:\ a number;
one of the four symbols {\tt +}, {\tt -}, {\tt *}, or {\tt /}; or a sublist
(such as the three-element list {\tt (3~+~4)} in this example) satisfying
the same rule. (You can imagine that we're implementing a pocket
calculator. If we were implementing a computer programming language, then
we'd also accept variable names as operands. But we're not bothering with
that complication because it doesn't really affect the part of the problem
about turning the expression into a tree.)
What makes this problem tricky is that we can't put the list elements into
the tree as soon as we see them. For example, the first three elements of
our sample list are {\tt 4}, {\tt +}, and {\tt 3}. It's tempting to build a
subtree of those three elements:
\pspicture{1in}{Tree for {\tt 4+3}}{fourplus}{}
\noindent But if you compare this picture with the earlier picture of the
correct tree, you'll see that the second argument to this {\tt +} invocation
isn't the number {\tt 3}, but rather the subexpression {\tt 3~*~7}.
By this reasoning you might think that we have to examine the entire
expression before we can start building the tree. But in fact we can
sometimes build a subtree with confidence. For example, when we see the
minus sign in our sample expression, we can tell that the subexpression
{\tt 3~*~7} that comes before it is complete, because {\tt *} has higher
precedence than {\tt -} does.
Here's the plan. The program will examine its argument from left to right.
Since the program can't finish processing each list element right away, it
has to maintain information about the elements that have been examined but
not entirely processed. It's going to be easier to maintain that
information in two parts:\ one list for still-pending operations and another
for still-pending operands. Here are the first steps in parsing our sample
expression; the program examines the elements of the argument, putting
numbers onto the operand list and operation symbols onto the operation
list:\footnt{Actually, as we'll see shortly, the elements of the operand
list are trees, so what we put in the operand list is a one-node tree whose
datum is the number.}
\def\tx{\TrimTop{0.25truein}}
\pspicture{100pt}{parsing tree to queues}{parse1}{\tx}
At this point, the program is looking at the {\tt *} operator in the infix
expression. If this newly seen operator had lower precedence than the {\tt
+} that's already at the head of the list of operations, then it would be
time to carry out the {\tt +} operation by creating a tree with {\tt +} at
the root and the first two operands in the list as its children. Instead,
since {\tt *} has higher precedence than {\tt +}, the program isn't ready to
create a subtree but must instead add the {\tt *} to its operation list.
\pspicture{52pt}{parsing tree to queues}{parse2}{\hSlide{-0.1truein}\tx}
This time, the newly seen {\tt -} operation has lower precedence than the
{\tt *} at the head of the operation list. Therefore, it's time for the
program to {\it handle\/} the {\tt *} operator, by making a subtree
containing that operator and the first two elements of the operand list.
This new subtree becomes the new first element of the operand list.
\pspicture{52pt}{parsing tree to queues}{parse3}{\tx}
Because the program decided to handle the waiting {\tt *} operator, it still
hasn't moved the {\tt -} operator from the infix expression to the operator
list. Now the program must compare {\tt -} with the {\tt +} at the head of
the list. These two operators have the same precedence. Since we want to
carry out same-precedence operators from left to right, it's time to handle
the {\tt +} operator.
\pspicture{65pt}{parsing tree to queues}{parse4}{\hSlide{-0.35truein}\tx}
Finally the program can move the {\tt -} operator onto the operator list.
The next several steps are similar to ones we've already seen.
{\hfuzz=30pt
\pspicture{150pt}{parsing tree to queues}{parse5}{\hSlide{-0.25truein}\tx}
}
This is a new situation: The first unseen element of the infix expression is
neither a number nor an operator, but a sublist. We recursively {\tt parse}
this subexpression, adding the resulting tree to the operand list.
\pspicture{65pt}{parsing tree to queues}{parse6}{\hSlide{0.075truein}\tx\TrimRight{0.5in}\TrimLeft{0.5in}}
Then we proceed as before, processing the {\tt /} because it has higher
precedence than the {\tt +}, then the {\tt -} because it has the same
priority as the {\tt +}, and so on.
\pspicture{260pt}{parsing tree to queues}{parse7}{\tx}
Once the program has examined every element of the infix expression, the
operators remaining on the operator list must be handled. In this case
there is only one such operator. Once the operators have all been handled,
there should be one element remaining on the operand list; that element is
the desired tree for the entire original expression.
\pspicture{90pt}{parsing tree to queues}{parse8}{\hSlide{0.1truein}\tx}
The following program implements this algorithm. It works only for correctly
formed infix expressions; if given an argument like {\tt (3~+~*)}, it'll give
an incorrect result or a Scheme error.
{\prgex%
(define (\ufun{parse} expr)
(parse-helper expr '() '()))
(define (parse-helper expr operators operands)
(cond ((null? expr)
(if (null? operators)
(car operands)
(handle-op '() operators operands)))
((number? (car expr))
(parse-helper (cdr expr)
operators
(cons (make-node (car expr) '()) operands)))
((list? (car expr))
(parse-helper (cdr expr)
operators
(cons (parse (car expr)) operands)))
(else (if (or (null? operators)
(> (precedence (car expr))
(precedence (car operators))))
(parse-helper (cdr expr)
(cons (car expr) operators)
operands)
(handle-op expr operators operands)))))
(define (handle-op expr operators operands)
(parse-helper expr
(cdr operators)
(cons (make-node (car operators)
(list (cadr operands) (car operands)))
(cddr operands))))
(define (precedence oper)
(if (member? oper '(+ -)) 1 2))
}
We promised that after building the tree it would be easy to compute the
value of the expression. Here is the program to do that:
{\prgex%
(define (\ufun{compute} tree)
(if (number? (datum tree))
(datum tree)
((function-named-by (datum tree))
(compute (car (children tree)))
(compute (cadr (children tree))))))
(define (function-named-by oper)
(cond ((equal? oper '+) +)
((equal? oper '-) -)
((equal? oper '*) *)
((equal? oper '/) /)
(else (error "no such operator as" oper))))
> (compute (parse '(4 + 3 * 7 - 5 / (3 + 4) + 6)))
30.285714285714
}
\subhd{Pitfalls}
\pit A leaf node is a perfectly good actual argument to a tree procedure,
even though the picture of a leaf node doesn't look treeish because there
aren't any branches. A common mistake is to make the base case of the
recursion be a node whose children are leaves, instead of a node that's a
leaf itself.
\pit The value returned by {\tt children} is not a tree, but a forest. It's
therefore not a suitable actual argument to a procedure that expects a tree.
\esubhd{Exercises}
{\exercise
What does
{\prgex%
((SAN FRANCISCO))
}
\noindent mean in the printout of {\tt world-tree}? Why two sets of
parentheses?
}
\solution
In general a tree node is a list whose {\tt car} is the datum and whose {\tt
cdr} is a list of the children. In the list {\tt ((SAN~FRANCISCO))}, the
{\tt car} is {\tt (SAN~FRANCISCO)} and the {\tt cdr} is {\tt ()}. So this is
a leaf node, since the list of children is empty. The inner parentheses
indicate that the datum is a list; the outer ones group the datum with its
(empty) children.
@
{\exercise
Suppose we change the definition of the tree constructor so that it
uses {\tt list} instead of {\tt cons}:
{\prgex%
(define (make-node datum children)
(list datum children))
}
How do we have to change the selectors so that everything still works?
}
\solution
The only change necessary is
{\prgex%
(define children cadr)
}
\noindent that is, use {\tt cadr} instead of {\tt cdr}.
@
{\exercise
Write {\tt \ufun{depth},} a procedure that takes a tree as argument and
returns the largest number of nodes connected through parent-child links.
That is, a leaf node has depth 1; a tree in which all the children of the
root node are leaves has depth 2. Our world tree has depth 4 (because the
longest path from the root to a leaf is, for example, world, country, state,
city).
}
\solution
{\prgex%
(define (depth tree)
(if (leaf? tree)
1
(+ 1 (reduce max (map depth (children tree))))))
}
@
{\exercise
Write {\tt \ufun{count-nodes}}, a procedure that takes a tree as argument
and returns the total number of nodes in the tree. (Earlier we counted the
number of {\it leaf\/} nodes.)
}
\solution
{\prgex%
(define (count-nodes tree)
(+ 1 (reduce + (map count-nodes (children tree)))))
}
@
{\exercise
Write {\tt \ufun{prune}}, a procedure that takes a tree as argument and
returns a copy of the tree, but with all the leaf nodes of the original tree
removed. (If the argument to {\tt prune} is a one-node tree, in which the
root node has no children, then {\tt prune} should return {\tt \#f} because
the result of removing the root node wouldn't be a tree.)
}
\solution
The need to eliminate branches that turn out to have no children
makes the solution a little inelegant. Here's Brian's inelegant
version:
{\prgex%
(define (prune tree)
(if (null? (children tree))
#f
(make-node (datum tree)
(filter (lambda (x) x)
(map prune (children tree))))))
}
\noindent and here's Matt's inelegant version:
{\prgex%
(define (prune any-tree)
(if (branch? any-tree)
(prune-branch any-tree)
#f))
(define (prune-branch branch)
(make-node (datum branch)
(map prune-branch (filter branch? (children branch)))))
(define (branch? node)
(not (null? (children node))))
}
@
\vfill\eject
{\exercise
Write a program {\tt \ufun{parse-scheme}} that parses a Scheme arithmetic
expression into the same kind of tree that {\tt parse} produces for infix
expressions. Assume that all procedure invocations in the Scheme expression
have two arguments.
The resulting tree should be a valid argument to {\tt compute}:
{\prgex%
> (compute (parse-scheme '(* (+ 4 3) 2)))
14
}
\noindent (You can solve this problem without the restriction to
two-argument invocations if you rewrite {\tt compute} so that it doesn't
assume every branch node has two children.)
}
\solution
The following procedure takes advantage of the fact that a valid
Scheme expression may not be empty. An ill-formed expression that
includes an empty subexpression will cause this procedure to blow up.
{\prgex%
(define (parse-scheme expr)
(if (word? expr)
(make-node expr '())
(make-node (car expr) (map parse-scheme (cdr expr)))))
}
Here's the modification to {\tt compute} suggested in the exercise:
{\prgex%
(define (compute tree)
(if (number? (datum tree))
(datum tree)
(apply (function-named-by (datum tree))
(map compute (children tree)))))
}
@
\bye



